. Kasia: Dane są funkcje kwadratowe f(x) = x2+4x+3 oraz g(x)= − x2+9 określone w zbiorze R. a) oblicz dla jakich argumentów obie funkcje przyjmują tę samo wartość . Ile ta wartość wynosi? b) rozwiąż graficznie nierówność f(x)>g(x) zad 2 funkcja kwadratowa f określona jest wzorem f(x)=12x2+0,8 x +c ,gdzie c jest liczba rzeczywistą.Funkcja ta ma jedno miejsce zerowe. a. wyznacz wartość współczynnika c b. rozwiąż nierówność | x−p|< 0,2 gdzie p jest odciętą wierzchołka paraboli funkcji f c. dla obliczonej wartości c wyznacz zbiór tych argumentów dla których wartości funkcji f są wiesze od wartości funkcji kwadratowej g jeśli g(x)=x2+0,32

Godzio: pomagam

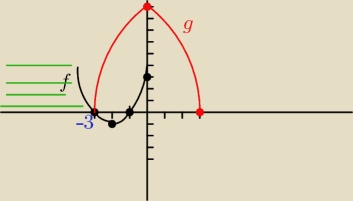
Godzio: a) x²+4x+3 = −x²+9 2x²+4x−6=0 Δ=16+48=64 √Δ=8 x₁=−3 x₂=1 b) f(x): Δ=16−12=4 √Δ=2

	−4
p=		=−2
	2

	−4
q=		=−1
	4

x₁=−3 x₂=−1 postać kanoniczna: f(x)=(x+2)²−1 g(x): Δ=0+36=36 √Δ=6 x₁=3 x₂=−3

	0
p=		=0
	−4

	−36
q=		=9
	−4

f(x)>g(x) −> x∊(−∞,−3)

Kasia: Dzięki .

Kasia: Mógłbyś spróbować zrobic drugie ?

Godzio: c obliczasz z tego że jest jedno rozw czyli Δ=0 Δ=b²−4ac b i a masz dane a Δ=0

	−b
p=		podstawiasz i obliczasz
	2a

majac to |x−p|<0,2 x−p<0,2 ∧ x−p>−0,2 c)tego nie jestem pewien ale spróbowałbym wykres narysować

Kasia: Jak byś mógł.