stożek opisany na kuli ninaxx: Na kuli o promieniu R opisano stożek ścięty. Średnica górnej podstawy stożka jest równa

3
	R. Znajdź pole powierzchni całkowitej stożka ściętego.
2

dero2005:

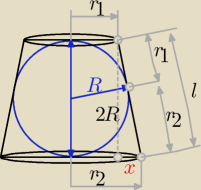
	3
r1 =		R
	4

r₂ = r₁ + x (r₁ + r₂)² = (2R)² + x² (³₄R + ³₄R + x)² = 4R² + x² (³₂R + x)² = 4R² + x^{2 9}₄R² + 3Rx + x² = 4R² + x² 9R² + 12Rx = 16R² 12Rx = 7R²

	7
x =		R
	12

	3		7		4
r2 = r1 + x =		R +		R =		R
	4		12		3

	25
l = r1 + r2 =		R
	12

P_c = π[r₁² + r₂² + l(r₁ + r₂)]

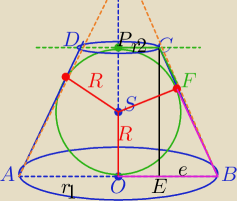Mila: AB=2r₁

	1		3		3
r2=		*		R=		R
	2		2		4

|CE|=2R

	3
|PC|=		R
	2

E, O − punkty styczności okręgu są jednakowo odległe od wierzchołków kątów.

	3		3
AD=BC=OB+PC=2*		R+e=		R+e
	4		2

w ΔCEB:

	3
e2+(2R)2=(		R+e)2
	2

	9
e2+4R2=		R2+3eR+e2
	4

	7
e=		R
	12

	3		7
r1=		R+		R
	4		12

	4
r1=		R
	3

Dalej stosuj wzory.