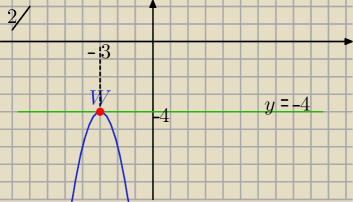
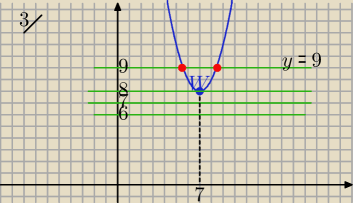
Funkcja kwadratowa Paola: Zadanie1 Funkcja kwadratowa g dla argumentów −4 i 14 przyjmuje tę samą wartość. Wobec tego osią symetrii wykresu funkcji g jest prosta o równaniu A. x = 0; B. x = 4; C. x = 5; D. x = 7. Zadanie2 Wykres funkcji g(x)=−2(x+3)²−4 ma dokładnie jeden punkt wspólny z prostą o równaniu A. y = −4; B. y = −3; C. y = −2; D. y = 3. Zadanie3 Parabola o równaniu y=(x−7)²+8 ma dwa punkty wspólne z prostą o równaniu A. y = 6; B. y = 7; C. y = 8; D. y = 9. Będę bardzo wdzięczna za odpowiedzi i obliczenia, żebym mogła to zrozumieć.

PW: Jednakowe wartości u funkcji kwadratowej osiągane dla −4 i dla 14 oznaczają, że punkty (−4, u) i (14, u) są położone symetrycznie względem pionowej prostej. Prosta ta dzieli odcinek na połowę, a więc przebiega przez punkt o pierwszej współrzędnej

	−4 + 14
		= 5.
	2

ann: z1 g(x)=ax²+bx+c g(−4)=g(14) stad otrzymasz rownanie z niewiadomymi a i b wylicz np a skorzystaj ze wzoru na wierzcholek paraboli i wstaw za a to co dostales z rownania wczesniej

ann: z2 tez ze wzoru na wiercholek paraboli, bo tylko w wierzchoku staa funkcja bedzie miala 1 pkt wspolny

ann: z3. parabola jest skierowana ramionami ku gorze bo przy x² jest dodatni wspoczynnik, wiec dwa punkty przeciecia bedzie miala z funkcja, która bedzie miala wart wieksze od wart paraboli w wierzcholku

Eta:

Eta: