d Jedno zadanko: √x+1 +1 < x

sprawdzcue czy dobrze: sprawdzcie czy dobrze zrobnilem to √x+1 +1 < x √x+1 < x−1 (do kwadratu) x +1 < x² +1 −x² +x < 0 x(x−1) >0 x = 0 v x=1 załozenie: x−1<0 x < 1

i-u: przy nierównościach, gdzie nie masz gwarancji, że obie strony nierówności są większe od 0, nie możesz podnosić obustronnie do kwadratu. Po drugie (x−1)² = x²−2x+1

.: √x+1 + 1 < x D = <−1; +oo) √x+1 < x −1 pierwiastek przyjmuje wartość <0;+oo) dla IR czyli nie może być mniejszy od 0 z tego wnioskumemy że x−1 > 0 czyli x > 1 L > 0 , P > 0 x+1 < x² −2x +1 0 < x² − 3x x=0 x=3 x E (−oo;0)u(3;+oo) z dziedziną równamy i mamy x E (3;+oo)

AS: poszukaj rozwiązania w poście dla KUBA

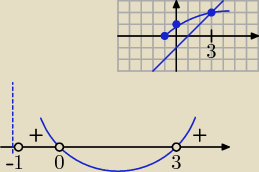
Bogdan: Założenie: x +1 ≥ 0 ⇒ x ≥ −1 √x + 1 + 1 < x √x + 1 < x − 1 /² x + 1 < x² − 2x + 1 (prawa strona − wzór skróconego mnożenia) x² − 3x > 0 ⇒ x(x − 3) > 0 x∊(3, +∞) (na górnym rysunku są wykresy: y = √x + 1, y = x − 1)

Magda: wiec zeby sprawdzic ze x > 0 to musze poprostu prawa strone przyrownac do 0 > ?