Oblicz pole obszaru ograniczonego przez krzywe Kaśka: Oblicz pole obszaru ograniczonego przez krzywe a) y=8/x y=1/8x y= √x b) y= e^x y= e⁻x y=4

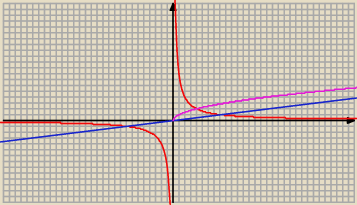
pigor: ..., a) odcięte x ≥0 punktów wspólnych krzywej y=⁸_x z dwoma pozostałymi to: ⁸_x= ¹₈x v ⁸_x= √x ⇔ x=8 v x= 4 , wtedy obszar między tymi 3−ema krzywymi, to P₁= ∫₀⁴ (√x − ¹₈x)dx + ∫₄⁸ (⁸_x − ¹₈x)dx= itd. licz ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− i na tym dla mnie mógłby być koniec, ale jest jeszcze x= 64 odcięta punktu wspólnego krzywych y=¹₈x i y=√x, bo ¹₈x=√x ⇒ x²−64x=0 ⇔ x(x−64) ⇔ x=0 v x=64, a wtedy obszar miedzy nimi to P= ∫₀⁶⁴(√x−¹₈x)dx= ... a zatem P₂= P−P₁= ... ale nie wiem, czy autorom zadania o to chodziło

Janek191: