Wyznacz monotoniczność, wypukłość i punkty przegięcia dla
justynka361: f(x)=2xln(2x−1)
17 gru 18:59
Radek: Zacznij od wyznaczenia dziedziny a potem od obliczenia pochodnej 1 i 2 rzędu
17 gru 19:02
Radek:
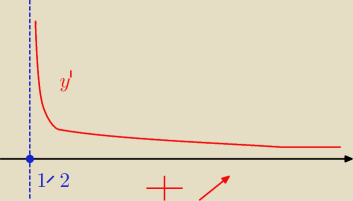
| | 4x | |
y'=(2xln(2x−1))'= |
| +2log(2x−1) |
| | 2x−1 | |
Dy'=Dy
y'=0
| | 4x | |
y'=(2xln(2x−1))'= |
| +2log(2x−1)=0 |
| | 2x−1 | |
Brak rozwiązania
17 gru 19:11
Radek:
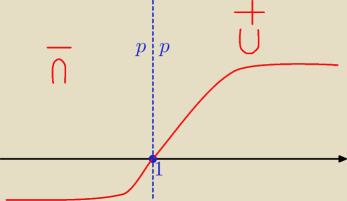
| | 8x−8 | |
y''=(2xln(2x−1))''= |
| |
| | (2x−1)2 | |
Dy''=Dy
y''=0
8x−8=0
8(x−1)=0
x=1
17 gru 19:16
justynka361: Dlaczego w monotoniczności wychodzi brak rozwiązania?
17 gru 19:22
Radek: Bo nie ma rozwiązania tego równania.
17 gru 19:27

