Liczba S jest sumą wszystkich liczb całkowitych aaron: Liczba S jest sumą wszystkich liczb całkowitych spełniających nierównośc: (x²−6x+5)(x²−60x+500)≤0 . Ile wynosi S. Prosze o pomoc

Mila: Rozwiąż nierówność− masz z tym problem?

aaron: nie. wychodzi x∊<1;5>∪<10;50> . tylko co dalej

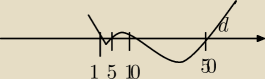
kyrtap: (x² − 6x +5)(x²−60x +500)≤0 x² − 6x + 5 = (x−1)(x−5) Δ = 36 − 4 * 5 = 16, √Δ = 4

	6 −4
x1 =		= 1
	2

	6+4
x2 =		= 5
	2

x² − 60x +500 = (x−10)(x−50) Δ = 3600 − 4 * 500 = 1600, √Δ = 40

	60 − 40
x3 =		= 10
	2

	60 + 40
x4 =		= 50
	2

(x² − 6x +5)(x²−60x +500)≤0 ⇒ (x−1)(x−5)(x−10)(x−50) ≤ 0 ⇒ x∊<1,5> ∪ <10,50> ⋀ x∊Z

Hajtowy: x²−6x+5 = (x−1)(x−5) x²−60x+500 = (x−10)(x−50) Czyli masz: (x−1)(x−5)(x−10)(x−50) ≤ 0

aaron: no ok. tylko wynik wychodzi S=1245 próbowałam z sumy ciągu arytmetycznego, ale też nie wychodzi... Może nie o to chodziło... nie wiem

Mila: x∊<1;5>∪<10;50> Teraz oblicz, ile jest całkowitych liczb i jakich w tych przedziałach domkniętych. {1,2,3,4,5} , tu liczymy sumę na piechotę: S₁=1+2+3+4+5=15 W przedziale <10,50> możesz obliczyć za pomocą ciągu arytmetycznego albo zdrowego rozsądku. a₁=10, r=1 a_n=50=10+(n−1)*1 n=41

	10+50
S41=		*41=30*41=1230
	2

S=15+1230 Sprawdź rachunki albo zgodność z odpowiedzią.

aaron: oo dziękuję ! źle wyliczyłam an z drugiego przedziału

Mila: