parametr Axel: Wyznacz wszystkie wartości parametru a , dla których równianie ||x+2|−3|=a−x ma nieskonczenie wiele rozwiązań

pigor: ..., np. tak : ||x+2|−3|=a−x ⇔ ||x+2|−3|+x=a i teraz 1) graficznie : narysuj wykres f(x)=||x+2|−3|+x i odczytaj z niego dla jakich wartości a∊R prosta y=a || OX ma ∞ wiele punktów wspólnych z tym wykresem (z częścią wykresu || do osi OX)... −−−−−−−−−−−−−−−−−−−−−−−−−− 2) a analitycznie może np. tak :

pigor: ..., wyznacz wszystkie wartości parametru a, dla których równianie ||x+2|−3|=a−x ma nieskończenie wiele rozwiązań. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− ||x+2|−3|=a−x i (*) a−x ≥0 ⇒ (|x+2|−3)²= (a−x)² ⇔ ⇔ (x+2)²−6|x+2|+9= a²−2ax+x² ⇔ x²+4x+4−6|x+2|+9= a²−2ax+x² ⇔ ⇔ 4x+2ax−6|x+2|= a²−13 ⇔ ⇔ (x<−2 i 4x+2ax+6x+12= a²−13) v (x ≥−2 i 4x+2ax−6x−12= a²−13) ⇔ ⇔ (x<−2 i 4x+2ax+6x= a²−25) v (x ≥−2 i 4x+2ax−6x= a²−1) ⇔ ⇔ (x<−2 i 2ax+10x= a²−25) v (x ≥−2 i 2ax−2x= a²−1) ⇔ ⇔ (x<−2 i (2a+10)x= a²−25) v (x ≥−2 i (2a−2)x= a²−1) ⇔ ⇔ (x<−2 i 2(a+5)x= (a−5)(a+5)) v (x ≥−2 i 2(a−1)x= (a−1)(a+1)) ⇔ ⇔ (x<−2 i a+5≠0 i 2x= a−5) v (x ≥−2 i a−1≠0 i 2x= a+1) , stąd i z (*) ⇔ ⇔ (a−5<−4 i a≠−5 i 2a−a+5 ≥0) v (a+1≥−4 i a≠1 i 2a−a−1 ≥0) ⇔ (a<1 i a≠−5 i a ≥ −5) v (a≥ −5 i a≠1 i a ≥1) ⇔ ⇔ −5<a<1 v a >1 ⇔ a∊−5;1) U (1;+∞) ...i tyle ufff... −−−−−−−−−−−−−−−−−− p.s. jak zwykle piszę online i ... nie ręczę głową za wynik w takim tasiemcu liczbowym i zainteresowanym radzę mnie sprawdzać krok po kroku. ...

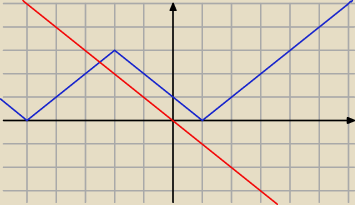
Gray: Moim zdaniem, nie ma ładniejszego rozwiązania tego zadania, jak rozwiązanie graficzne. Ponieważ funkcja prawej stron wygląd tak jak wygląda − da się to rozwiązanie dokładnie uzyskać. Na rysunku na niebiesko zaznaczyłem funkcję prawej strony; na czerwono wykres funkcji y=−x. Aby treść zadania była spełnione muszę tak przesunąć czerwone aby pokryło się z niebieskim: stąd a=1 lub a=−5. pigor − wytrwały jesteś

PW: A ja jak zwykle wolę pogadać. Niezależnie od przedziału, na którym rozpatrujemy badane równanie, ma ono postać (1) sx + b = a − x, gdzie s = −1 lub s = 1. Jest to więc równanie liniowe. Równanie takie ma nieskończenie wiele rozwiązań tylko wtedy, gdy s = −1 i b = a. Jak łatwo zauważyć współczynnik s przy x w wyrażeniu ||x+2| − 3| jest ujemny, gdy 1° x+2 ≥ 0 i jednocześnie x+2−3 < 0, wtedy −2 ≤ x < −1, zaś występujący w (1) współczynnik b jest równy +1 albo 2° x+2 < 0 i jednocześnie −x−2−3 ≥ 0, wtedy x ≤ −5, zaś współczynnik b jest równy −5. Odpowiedź: Równanie ma nieskończenie wiele rozwiązań, gdy a = 1 lub a = −5. Sprawdzenie. Dla a = 1 równanie ma postać ||x+2| − 3| = 1 − x, ma ono nieskończenie wiele rozwiązań dla x∊[−2, −1), gdyż na tym przedziale przyjmuje postać |x − 1| = 1 − x, czyli −x + 1 = 1 − x. Dla a = −5 równanie ma postać ||x+2| − 3| = −5 − x, ma ono nieskończenie wiele rozwiązań dla x∊(−∞, 5], gdyż na tym przedziale przyjmuje postać |−x−2−3| = − 5 − x, czyli |x+5| = −5 − x, to znaczy − x − 5 = − 5 − x.

PW: Zajęty byłem czym innym i nie widziałem rozwiązania Graya, ale ciszę się, że jesteśmy zgodni.