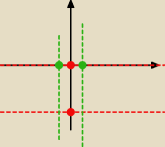
ekstremum globalne/obszar/punkty stacjonarne ryba: przy obliczani ekstremum globalnego mam funkcje z=x³+8y³−6xy ograniczoną takim obszarem: D:{(x,y): 0≤x≤4, −1≤y≤1} pierwszy punkt stacjonarny to wiadomo że z układu równań pochodnych cząstkowych. problem tkwi w tym, że nie wiem jak obliczyć kolejne punkty z tego obszaru. wykombinowałem, że: x∊<0,4> y∊<−1,1> co zobrazowałem na rysunku (nie wiem czy poprawnie) proszę o dalsze wskazówki

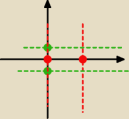
ryba: jednak wydaje mi się, że rysunek powinien być taki:

ryba: ponawiam pytanie. a jak z tym obszarem? który jest poprawny?

Gray: Jeżeli pozioma oś to Ox, a pionowa to Oy, to drugi rysunek jest dobry. Z wnętrza obszaru wybierasz tylko te, w których zerują się obydwie pochodne cząstkowe (wyznaczyłeś je?). Następnie badasz funkcję na brzegu obszaru − to cztery odcinki. Na brzegu funkcja staje się funkcją jednej zmiennej, więc masz zadanie dużo prostsze; algorytm ten sam − zerowanie się pochodnej. Na koniec dołączasz cztery wierzchołki (0,−1), (0,1), (4,−1), (4,1). I szukasz teraz wartości najmniejszej i największej w tak wyznaczonych punktach.

ryba: taka odpowiedź jest dla mnie jasna i konkretna, dziękuję bardzo

ryba: ah jeszcze drobne pytanie, te cztery odcinki (brzegi) x=1 x=−1 y=0 y=4 dla jakich przedziałów x i y? bo nie rozumiem jak to się wyznacza.

Gray: Patrz na rysunek. Co jest brzegiem obszaru? Cztery odcinki. Oto one: a) x=0, y∊[−1,1] b) x∊[0,4], y=1 c) x=4, y∊[−1,1] d) x∊[0,4], y=−1.

ryba: już rozumiem. wcześniej wyobrażałem sobie zamiast odcinków równania prostych dlatego nie mogłem pojąć skąd się biorą te przedziały. dzięki raz jeszcze.

Gray: Interesują Cię tylko te fragmenty prostych, które zawarte są w obszarze na którym szukasz wartości ekstremalnych.