pole całkowite i objętość garniastosłupa prostego honeyangel: Zad. 1 Podstawą graniastosłupa prostego jest trójkąt równoboczny o boku długości a. Miara kąta między przekątną ściany bocznej a krawędzią boczną wynosi α. Oblicz objętość tego graniastosłupa. Zad. 2 Podstawą graniastosłupa prostego jest kwadrat. Miara kątów miedzy przekątna podstawy a przekątną graniastosłupa wynosi α. Oblicz pole powierzchni tego graniastosłupa, jeśli jego wysokość ma długość h.

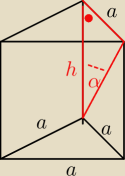
Janek191: Mamy

a		a
	= tg α ⇒ a = h tg α ⇒ h =
h		tg α

	a2 √3		a		a3 √3
V = Pp*h =		*		=
	4		tg α		4 tg α

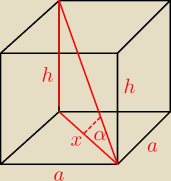
Janek191: Mamy

	x		x2
x = a√2 ⇒ a =		⇒ a2 =
	√2		2

h		h		h2
	= tg α ⇒ h = x tg α ⇒ x =		⇒ x2 =
x		tg α		tg2 α

więc

	h2		h
a2 =		⇒ a =
	2 tg2 α		√2 tg α

Pole powierzchni graniastosłupa P_c = 2 P_p + P_b = 2 a² + 4 a*h

	h2		h		h2		4 h2
Pc =		+ 4*		*h =		+		=
	tg2α		√2*tg α		tg2α		√2 tg α

	1		4		h2
= [		+		]*
	tg α		√2		tg α