Oblicz pole trójkąta równobocznego
husariusz:
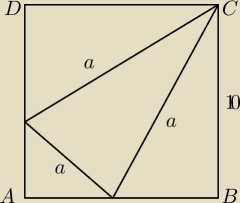
W Kwadrat o boku 10 cm wpisano trójkąt równoboczny CEF. Oblicz jego pole
15 gru 23:48
Mila:
Nie widzę, aby to był Δ równoboczny.
15 gru 23:50
15 gru 23:51
Eta:
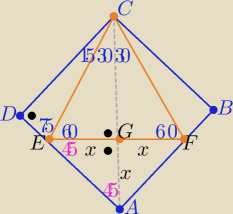
2x−−− dł. boku trójkąta
|CF|=x
√3 , |AF|=x , |AC|=10
√2
x
√3+x= 10
√2 ⇒ x(
√3+1)=10
√2 /* (
√3−1)
2x=10
√2(
√3−1)
| | (2x)2√3 | |
P(EFC)= |
| = x2*√3= ............ |
| | 4 | |
16 gru 00:28
husariusz: Rozumiem, ale chyba |CG|=x√3, a nie CF
16 gru 00:41
Eta:
Tak |CG|=x√3
16 gru 00:42
husariusz: Dzięki serdeczne za pomoc.
16 gru 00:44
Eta:
I jeszcze |AG|= x
Sorry za pomyłkę
16 gru 00:45
Mila:
W ΔCDE (rysunek
Ety:
a− bok Δ równobocznego
a*(
√6+
√2)=40 /*(
√6−
√2)
a*4=40*(
√6−
√2)
a=10*(
√6−
√2)
16 gru 20:32
