pole trójkąta- zadanie esia: Proszę o wytłumaczenie rozwiązanego zadania Stosunek długości ramienia trójkąta równoramiennego do jego obwodu wynosi 0,3. Pole trójkąta jest równe 8√5. Oblicz długości boków tego trójkąta. b/a+2b=0,3 b=0,3+0,6b 0,4b=0,3a b=3/4a a=4/3b obliczam h (a/2)² + h²= b² (2/3b)²+h²=b² h²=b²− 4/9 b² h²=5/4b² h=√5 /3b później obliczam b... zadanie mam dobrze rozwiązane tyle że nie rozumiem skąd się wzięło h²=5/4b² a później h=√5 /3b. Prosze o wytłumaczenie

:):

	a		3		10
jeśli		=		, to L=		a
	L		10		3

	2
po podstawieniu do obwodu b=		a
	3

cos masz nie tak

:): sorki, źle zerknęłam, a i b masz ok

:):

	4		9		4
1−		=		−
	9		9		9

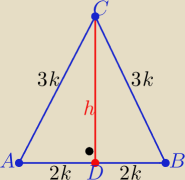
Eta: Pokażę taki sposób rozwiązania tego zadania:

	|AC|		3
Z treści zadania:		=
	Ob		10

to Ob=10k , |AB|=4k , |AC|=|BC|=3k , k>0 Z tw. Pitagorasa h=√9k²−4k²= √5*k P= 2k*h ⇒ 2√5k²=8√5 ⇒ k²=4 ⇒ k=2 to: |AB|=4k=8 , |AC|=|BC|=3k= 6

esia: dziękuje wam bardzo