Pole trójkąta- zadanie esia: W trójkącie równoramiennym wysokość opuszczona na podstawę jest od niej o 2 cm krótsza. Oblicz pole tego trójkąta, jeżeli jego obwód wynosi 16 cm. a=h+2 obw=2b+h+2 16=2b+h+2 2b=16−h−2 2b=14−h b=7− h/2 (h+2)²/4+ 4²= (7− h/2)² h² + 4h+4/4 + 4h/4= 49−7h + h²/4 h² +h+1+7h−49=0 dalej wyliczam delte h1 i h2 a później pole. Problem polega na tym że nie rozumiem skąd wzięły się te dwie linijki działań pod wyliczeniem b. Bardzo prosze o pommoc

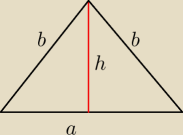
Janek191: a = h + 2 b² = h² + (0,5 a)² = h² + (0,5 h + 1)² = h² + 0,25 h² + h + 1 = 1,25 h² + h + 1 a + 2 b = 16 a + 2√1,25h² + h + 1 = 16 2√ 1,25 h² + h + 1 = 16 − a = 16 − ( h + 2) = 14 − h Podnosimy do kwadratu 4*( 1,25 h² + h + 1) = 196 − 28 h + h² 4 h² + 32 h − 192 = 0 / : 4 h² + 8 h − 48 = 0 Δ = 64 − 4*1*( −48) = 64 + 192 = 256 √Δ = 16

	− 8 + 16
h =		= 4
	2

a = 4 + 2 = 6 więc pole P = 0,5*6*4 = 12 [ cm²] ==============

esia: dziękuję !

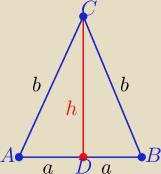Eta: Unikamy ułamków, wprowadzając takie oznaczenia jak na rys. |AB|=2a , i h= 2a−2 2b+2a=16 ⇒ a+b= 8 ⇒ b= 8−a , a∊(0,8) z tw. Pitagorasa a²+(2a−2)²=(8−a)² ⇒ a²+2a−15=0 ⇒(a−3)(a+5)=0 ⇒ a=3 h= 2a−2= 6−2=4 P= a*h= 3*4=12 cm²