.... Hondziarz: Wyznacz współrzędne punktu P równoodległego od punktów A(−9; 2) i B(3; 8) oraz od prostej k: 2x−y−4=0

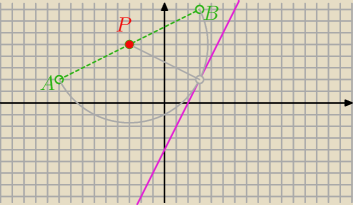
Tadeusz: Ten punkt to środek odcinka AB

Hondziarz: Faktycznie, wystarczyło narysować i wszystko jasne. Dzięki Tadziu

Hondziarz: A czy tu będzie jeszcze jakiś przypadek oprócz tego?

Tadeusz: ... nawet ten przypadek powinieneś policzyć Inny sposób to dowód, że nie ma innej możliwości −

Hondziarz:

	9
Policzyłem, ale coś nie do końca wyszło. P(−3, 5) lub P(		, −10) o odpowiedziach ten drugi
	2

jest inny

Tadeusz: ... nie wiem jak to liczyłeś

pigor: ..., , no to szukaj analitycznie np. tak : niech P=(x,y)=?, to warunki zadania spełnia np. taki układ równań : (x+9)²+(y−2)²= (x−3)²+(y−8)² = ¹₅|2x−y−4|² ⇔ ⇔ (x+9−x+3)(x+9+x−3)=(y−8−y+2)(y−8+y−2) i (*) 5(x−3)²+5(y−8)²=(2x−y−4)² ⇒ ⇒ 12(2x+6)= −6(2y−10) /:12 ⇔ 2x+6= 5−y ⇔ (**) y= −2x−1 , stad i z (*) : 5(x−3)²+5(−2x−9)²= (4x−3)² ⇔ 5(x²−6x+9)+5(4x²+36x+81)= 16x²−24x+9 ⇔ ⇔ 25x²+150x+450−16x²+24x−9= 0 ⇔ 9x²+174x+441= 0 i sprawdź, że środek odcinka AB S_AB= (−3,5) spełnia to równanie ; liczymy dalej Δ= 174²−4*9*441= 174²− (6*21)²= (174−126)(174+121)= 48*295= 16*3*5*59 , to √Δ= 4√885 i 0> x= ¹₁₈(−174−4√885), a więc coś tam jeszcze istnieje, i ile się gdzieś nie ,...

pigor: ,, no właśnie ten S_AB=(−3,5) taki ładny, spełnia to brzydkie równanie, którego Δ>0 , ale taka brzydka, chyba więc gdzieś sie w niej walnąłem ,

Tadeusz: Proponuję troszkę inaczej Punkt P musi leżeć na symetralnej odcinka AB Środek odcinka S=(−3,5) wsp. kierunkowy prostej przez A i B a=1/2 równanie symetralnej y=−2x−1 P=x_p, −2x_p−1) |AP|=√5(x_p+6x_p+18) odległość P od prostej 2x−y−4=0

	|2xp+2xp+1−4|
d=		|4xp−3|=5√xp+6xp+18
	√4+1

a z tego (x_p+3)²=0 ⇒ x_p=−3 Zatem P=S

Eta: Mnie wyszła taka odp: ( jak się gdzieś nie pomyliłam w rachunkach

	1		2
P(−3,5) , P(−16		,32		)
	3		3

Masz może odpowiedź do tego zadania?

Eta: Mam takie samo równanie jak podał pigor y= −2x−1 9x²+174x+441=0 /:3 3x²+58x+147 , Δ= 1600 , √Δ= 40

	98		1
x= −3 v x= −		= −32		to y=...........
	6		3

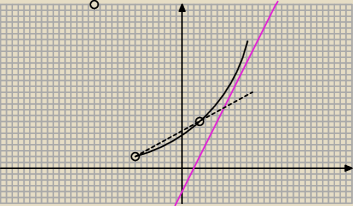
Tadeusz: ... i jak zwykle masz rację−

Eta: Poprawiam chochlika

	98		1
x=−		= −16
	6		3

pigor: ..., tu 13:37 w liczeniu Δ = ...= (174−126)(174+121)= ... w 3−ej linii od końca mam błąd nieuwagi, powinno być (174−126)(174+126) = ...

Eta: Wniosek : nieraz warto liczyć deltę ( bez kombinowania

x: δγβα

deg: skąd 1/5 przy module z 2x−y−4?

zzlk: Ze wzoru na odległość punktu od prostej. W module otrzymujemy √5. Jest to promień, czyli podstawiając do wzoru okręgu potrzebujemy podnieść do kwadratu promień, czyli potrzymamy 5.

7uyjk: ←←←←←⇒⇒⇒⇔⇔⇒∫∊

7uyjk: kurcze przez przypadek to wyslalem, nie wiem jak usunąć. NA LEB JUZ DOSTAJE OD TEJ MATEMTYKI, PODDAJE SIE

Mila: Przestań się wygłupiać.