Nie mam pomysłu :/ dyzio: Wykaż, że jeśli zbiorem wartości funckji kwadratowej f(x) = −x² + 2kx − 3 jest przedział (−∞;1>, to k∊R

zapora: a nie pomyliłeś nic? żadnego minusa?

dyzio: sory ! to ∊ {−2;2} tu jest jedyny błąd

zapora: no to teraz możesz policzyć wiedząc z treści zad, że q=1 i samo wyjdzie

Eta: x_w= k y_w= 1

	b
yw= c+		*xw = −3+k*k = k2−3
	2

to k²−3=1 ⇒ k²−4=0 ⇒ k=2 v k= −2

dyzio: co to jest za wzór który używasz w drugiej lini ?

dyzio: ?

Eta:

	−b
xw=
	2a

	−Δ		b
yw= f(xw) lub yw=		lub yw=c+		*xw lub yw= c−a*xw2
	4a		2

dyzio: Nie znam tych dwóch wzorów ale teraz rozumiem dzięki

Eta: Nie musisz ich znać ( ale ja znam , bo wtedy nie muszę liczyć delty Wyprowadzenie tego wzoru

	−Δ		−b2+4ac		b		−b		b
yw=		=		= c+		*		= c+		*xw
	4a		4a		2		2a		2

lub

	b2		b2
yw= c −		= c −a*		= c −a*xw2
	4a		4a2

dyzio: A pomogłabyś mi z jeszcze jednym zadaniem ?

Eta: Dawaj

dyzio: Dla jakich wartości parametru m równanie x² + mx + m = 0 ma dwa różne rozwiązania mniejsze od 2

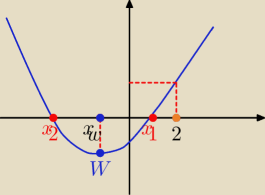
Eta: Parametr "m" musi spełniać układ warunków 1^o Δ>0 2^o f(2)>0

	−b
3o xw=		<2
	2a

rozwiąż i jako odp: podaj część wspólną tych rozwiązań

dyzio: 1* △ > 0 ⇔ m ∊ (−∞; 0) ∪ (4; +∞) tak mi wyszło

dyzio: 2* f(2) > 0 4 + 2m + m > 0 3m > −4

	1
m > −1
	3

Eta: dyzio .... licz tak, abyś był pewny swoich obliczeń! Kogo zapytasz na maturze?

dyzio: 3*

	m
xw = −		< 2 /* (−2)
	2

m > − 4 m ∊ (−4 ; +∞)

	1
m ∊ (−1		; 0) ∪ (4;+∞)
	3

dyzio: oki będę pamiętał

dyzio: Dobrze zrobiłem ?

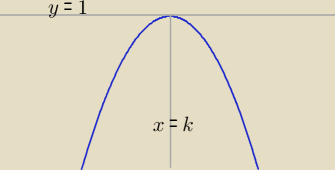
Bogdan: Zadanie 1. y = −x² + 2kx − 3, y_w = 1

	−2k
Oś symetrii paraboli x = xw =		= k
	−2

Postać kanoniczna y = −(x − k)² + 1 ⇒ y = −x² + 2kx − k² + 1, −k² + 1 = −3 ⇒ k² = 4

Eta:

Eta:

dyzio: Dzięki za pomoc ! Dobranoc