Stopy - stosunki martynka21: Dane są 2 stopy − miedź i cynk, w pierwszym stopie stosunek tych metali wynosi 1:2. a w drugim 2:3. Ile kilogramów każdego z tych stopów należy użyć, by otrzymać 10kg stopu o miedzi i cynku w stosunku p. Proszę o pomoc. Kompletnie nie wiem jak się za to zabrać.

O::

m		1
	+		⇒ c=2m
c		2

m		2		3
	=		⇒c=		m
c		3		2

(m+c)₁+(m+c)₂=10 I stop II stop wstaw za c i policz m

O::

	1
*=		zamiast +
	2

martynka21: Ale trzeba otrzymać to w stosunku p.

IQ: a to brzydko

martynka21: Odpowiedzi powinny wyjść:

30(2−2p)
	kg,
p+1

50(2p−1)
	kg
p+1

Proszę o pomoc

IQ: Ustalmy fakty: miedź i cyna to nie są stopy W pierwszym stopie jest 2x wiecej cyny niż miedzi., a w drugim 1,5x więcej wiec jak sie weźmie np. x kg pierwszego stopu, to drugiego trzeba wziąć 10 − x kg a stosunek miedzi do cyny ma być p = U{masa miedzi z pierwszego stopu+ masa z drugiego}{masa cyny z pierwszego+ drugiego} zastosuj to teraz

martynka21: Nie bardzo wiem jak to zastosować.

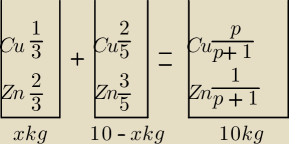Gustlik: Dane są 2 stopy − miedź i cynk, w pierwszym stopie stosunek tych metali wynosi 1:2. a w drugim 2:3. Ile kilogramów każdego z tych stopów należy użyć, by otrzymać 10kg stopu o miedzi i cynku w stosunku p. Metoda kubełkowa: W naczyniu 1 stosunek miedzi Cu do cynku Zn wynosi 1:2, czyli mamy 1 część Cu i 2 części Zn,

	1		2
razem 3 części, stąd Cu=		, a Zn=		, analogicznie w naczyniu 2 Cu mamy 2 części, a
	3		3

	2		3
Zn 3 części, stąd Cu=		, a Zn=		, bo razem części jest 5.
	5		5

	Cu		p
Po zmieszaniu stopów mamy stosunek		=p=		, czyli Cu jest p części, Zn jest 1
	Zn		1

	p		1
część, razem części jest p+1, stąd Cu=		, Zn=		.
	p+1		p+1

Rozwiążę równanie tak, jakbym liczył "stężenie" cynku w stopie:

2		3		1
	x+		(10−x)=10		/*15
3		5		p+1

	1
10x+9(10−x)=150
	p+1

	1
10x+90−9x=150
	p+1

	1
x=150		−90
	p+1

	150
x=		−90
	p+1

	150−90(p+1)
x=
	p+1

	150−90p−90
x=
	p+1

	60−90p
x=
	p+1

	30(2−3p)
x=		− I stop
	p+1

	60−90p		10(p+1)−60+90p
10−x=10−		=		=
	p+1		p+1

	10p+10−60+90p		100p−50		50(2p−1)
=		=		=		− II stop
	p+1		p+1		p+1

	30(2−3p)		50(2p−1)
Odp:		− I stop,		− II stop
	p+1		p+1