Parametry Metis: Cześć Brakuje mi jakiegoś warunku: Dla jakich wartości parametru m równanie x² + (m+2)x−2m+1 ma 2 rozwiązania rzeczywiste, z których jedno jest ujemne, a drugie większe od 1. Założenia: Δ>0 x₁*x₂<0 O czym zapomniałem ?

Tadeusz: f(1)<...

Metis: Podobny zapis znalazłem na matematyka.pl ale go nie rozumiem

Gray: Zobacz na rysunku jak musi wyglądać parabola spełniająca warunki zadania. Zrozumiesz dlaczego warunek f(1)<... załatwia sprawę.

Metis: Na sprawdzianie nie bede mógł rysować zadnej paraboli. Napiszcie mi proszę jak mogę inaczej zapisać warunek f(1) < ... i skąd owy warunek się bierze.

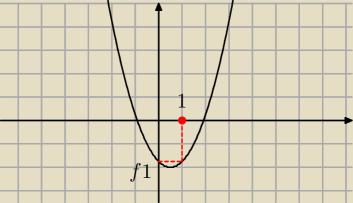
razor: współczynnik przy x² = 1 > 0 czyli parabola ma ramiona do góry Żeby jeden z pierwiastków był większy od 1 musi być spełniony warunek f(1) < 0 bo gdyby było f(1) > 0 to pierwiastek byłby mniejszy od 1 Drugi pierwiastek jest ujemny z warunku x₁*x₂ < 0

Tadeusz: ... a na sprawdzianie rysunek poglądowy nigdy zabroniony nie jest (ba ... wręcz zalecany)

Metis: Prawda ale chodzi o czas

Metis: razor

Metis: Kolejne: Narysuj wykres funkcji f(x)= −x * |x−2| f(x)= −x * (x−2) dla x≥2 −x* (−x+2) dla x<2 Upraszam, otrzymuje −x²+2x dla x≥2 x²−2x dla x<2 Jak teraz zbudować wykres funkcji ?

3Silnia&6: narysowac pierwszy wykres dla x ≥ 2 i druga dla x < 2.

Metis: Mało odkrywcze dzięki , a jak po narysowaniu mogę sprawdzić czy wykres wygląda tak jak powinien , jest dobrze narysowany ?

Mila: Wszystko zależy od funkcji. Można tak: Sprawdzasz w punkcie zmiany wzorów, a następnie kilka argumentów z lewej i prawej strony.

Metis: Dziękuje Milu za odpowiedź. We wtorek piszę sprawdzian z funkcji kwadratowej i na pewno pojawi sie zadanie z narysowaniem wykresu funkcji z modułem i jego analiza , w zależności od parametru. A niestety nie idą mi te wykresy A metoda algebraiczna niestety na lekcje za długa .