prosze bardzo o pomoc w takim zadaniu
romek: Odcinek AB gdzie A(1,3) i B(7,−3) jest podstawą trójkąta ABC, oblicz współrzędne punktu C tak
aby trójkąt ABC był równoramienny a jego pole było równe 30
18 lis 21:46
Eta:
Pomagam
....rysuję ..... to potrwa ( mam nadzieję ,że się w miarę szybko wgra)
Bardzo lubię geometrię analityczną
19 lis 00:14
Eta:
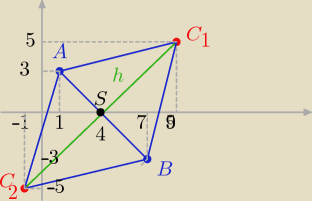
podstawa IABI =
√(1−7)2+(3+3)2=
√2*36=6
√2
wyznaczamy środek odcinka AB:
więc
S(4,0)
ISCI= h
AB
P
ΔABC=
12*IABI*h => 3
√2*h = 30=>
h= 5√2
Piszemy r ównanie prostej zawierajacej wysokość i jednocześnie punkty S i C
znajdujemy współczynnik kierunkowy prostej AB do której wysokość jest prostopadła
| | yA−yb | | 3+3 | |
aAB= |
| = |
| = −1
|
| | xA−xB | | 1−7 | |
więc współczynnik kier. prostej SC jest a
SC= 1
zatem: pr. SC: y−y
S= 1*(x −x
S)
pr.SC:
y = x −4
poniewaz punkt C (x,y) nalezy do niej to C( x, x−4)
teraz ISCI = h = 5
√2
ISCI
2= ( x
C−x
S)
2 +(y
C−y
S)
2
(x −4)
2+ ( x −4 −0)
2= (5
√2)
2
(x−4)
2 + ( x−4)
2 = 50
2(x −4)
2= 50 /:2
(x −4)
2= 25 => x−4 = 5 v x −4 = −5
to x = 9 v x = −1
więc y= x −4 => dla x= 9 y= 5 dla x= −1 y= −5
więc są dwa takie punkty C spełniajace warunki zadania:
odp:
C1( 9,5) C2( −1, −5)
Co też widać na rysunku w układzie współrzednych.
Dobranoc Wszystkim
idę
19 lis 00:48
AROB: Ja też idę
. Spokojnej nocy! Do jutra!
19 lis 01:12
19 lis 01:21
