rachunek róż.
Blue: | | 9 | |
zad.3 Wyznacz przedziały monotoniczności i ekstrema lokalne funkcji f(x) = 4x+ |
| . |
| | x | |
W odpowiedziach mam ekstrema jako punkty, ale czy ekstremum to nie jest sama wartość

? W tym
przypadku minimum −12 i maximum 12

?
14 gru 11:24
Janek191:
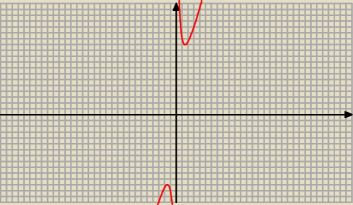
14 gru 11:26
Janek191:
Z wykresu wynika, że f ma maksimum lokalne równe −12 i minimum lokalne
równe 12

14 gru 11:27
Blue: no czyli dobrze mówię, że to nie są punkty

W odpowiedzi jest błąd

14 gru 11:31
Blue: no ale jest inaczej maximum to −12, a minimum to 12 racja

14 gru 11:32
Janek191:
| | 9 | | 9 | |
f'(x) = 4 − |
| = 0 ⇔ 4 = |
| ⇔ x = − 1,5 lub x = 1,5 |
| | x2 | | x2 | |
| | 9 | |
f( − 1,5) = 4*(−1,5) − |
| = − 6 − 6 = − 12 |
| | −1,5 | |
| | 9 | |
f(1,5) = 4*1,5 + |
| = 6 + 6 = 12 |
| | 1,5 | |
14 gru 11:34
Janek191:
Dana funkcja ma maksimum lokalne w punkcie x1 = −1,5 i minimum lokalne
w punkcie x2 = 1,5
oraz
ymax = − 12 i ymin = 12
14 gru 11:37
Blue: ok, dzięki

14 gru 13:03
 ? W tym
przypadku minimum −12 i maximum 12
? W tym
przypadku minimum −12 i maximum 12 ?
?


 W odpowiedzi jest błąd
W odpowiedzi jest błąd 

