Znaleźć naturalną dziedzinę i zbiór wartości Johny: Znaleźć naturalną dziedzinę D i zbiór wartości funkcji ZW: f(x)= U{−4}/{(x−5)(x+6)}

Johny:

	−4
f(x)=
	(x−5)(x+6)

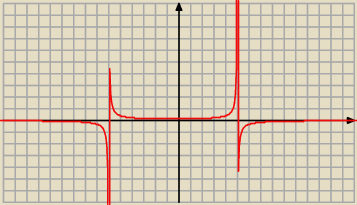
Gustlik: Dziedzina: mianownik ≠ 0 czyli (x−5)(x+6) ≠0 ⇔ x≠5 i x≠−6 ⇔ D=R\{−6, 5} zbiór wartości − jesteś na rozszerzeniu czy podstawach? Bo najlepiej byłoby to zbadać przy pomocy granic i ewentualnie pochodnych. Tak wygląda wykres tej funkcji, widać, że ZW=R\{0}, ale na piechotę ciężko to wyznaczyć.

Johny: Rozszerzenie, dawaj śmiało jak z granic

Gustlik: Zbadaj granice jednostronne w punktach nie należących do dziedziny, czyli w 5 i −6 praz zbadaj granicę w + i −∞. Wg mnie ZW=R\{0}.

pigor: ... , oj ... czyżby

	−4
f(x)=		i Df=R\{−6,5} − dziedzina naturalna f i w niej
	(x−5)(x+6)

	−4
jej wartość y=		⇔ y(x−5)(x+6)= −4 ⇔ y(x2+x−30)+4=0 ⇒
	(x−5)(x+6)

⇒ równanie yx²+yx+4−30y=0 i (y=0 v y≠0) ma pierwiastek(ki) ⇔ ⇔ (*) y≠0 i Δ= y²−4y(4−30y) ≥0 ⇔ y²−16y+120y² ≥0 ⇔ ⇔ 121y²−16y ≥0 ⇔ 121y(y− ¹⁶₁₂₁) ≥0 , a stąd i z (*) ⇔ ⇔ y<0 v y ≥ ¹⁶₁₂₁) ⇔ y∊(−∞;0) U < ¹⁶₁₂₁;+∞)=Z.W.. ...