nauka równań i nierówności baca: Mam takie przykłady do zrobienia i nie wiem kompletnie jak się za nie zabrać możecie to wytłumaczyć i rozwiązać ?

	1		x
1. rozwiąż równanie		+		−1=0
	x−3		6−2x

	3x−4
2.rozwiąż nierówność		≤5
	x−1

PW: 1. bardzo łatwe, wystarczy zauważyć, że 6 − 2x = 2(3 − x) = − 2(x − 3), a więc dodawanie ułamków po lewej stronie nie powinno sprawić kłopotu. Zacząć od ustalenia dziedziny − jakie nie mogą być iksy z powodu mianowników?

O:: sprowadź ułamki do wspólnego mianownika

baca: x≠5 ?

Janek191: x ≠ 3

baca: a co z −2 ? −2(x−3)=0 x−3=2 x=2+3 x≠5

Janek191: Co to za herezje wypisujesz ?

PW: Oj, baca, Ty zdaje się nic nie umiesz, takiemu trudno pomóc.

baca: czyli nie bierze się jej pod uwagę podczas wyznaczania ?

Janek191: 6 − 2x = 0 ⇔ 6 = 2x / : 2 3 = x więc dziedzina D = ℛ \ { 3} =========

baca: To rozumiem już tylko co dalej co z tą −1 i jak to dalej robić?

baca: rozwiążcie mi w całości te dwa przykłady

baca:

−x2+3x		2x−6		−x2+3x		x2−1		x(x+3)
	:		=		*		=
x−1		x2−1		x−1		2x−6		x−1

	x(x−1)		x2
*		=
	2(3−x)		2

to inny przykład ale chcę wiedzieć czy dobrze zrobiłem

Janek191:

1		x
	+		− 1 = 0
x − 3		6 − 2x

1		x
	+		− 1 = 0 ; x ≠ 3
x − 3		−2*( x − 3)

1		− x
	+		− 1 = 0
x − 3		2*(x − 3)

2		− x		2*(x −3)
	+		−		= 0
2*( x − 3)		2*(x − 3)		2*(x − 3)

2 − x − 2*( x − 3)
	= 0
2*( x − 3)

2 − x − 2 x + 6 = 0 − 3 x + 8 = 0 − 3 x = − 8 / : ( − 3)

	8
x =
	3

=======

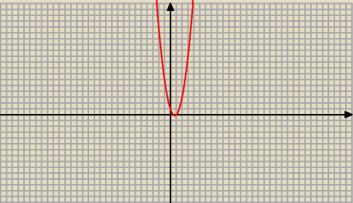
Janek191: 2)

3 x − 4
	≤ 5 ; x ≠ 1 ; mnożymy obustronnie przez ( x − 1)2
x − 1

(3 x − 4)( x − 1) ≤ 5*( x − 1)² 3 x² − 3 x − 4 x + 4 ≤ 5*( x² − 2 x + 1) 3 x² − 7 x + 4 ≤ 5 x² − 10 x + 5 − 2 x² + 3 x − 1 ≤ 0 / * ( −1) 2 x² − 3 x + 1 ≥ 0 Δ = (−3)² − 4*2*1 = 9 − 8 = 1

	3 − 1		2		1
x1 =		=		=
	4		4		2

	3 + 1
x2 =		= 1
	4

więc

	1
x ∊ ( − ∞;		> ∪ < 1; + ∞ )
	2

==========================

Janek191: Pomyłka: 1 ∉ D więc x ∊ ( − ∞ ; 0,5 > ∪ ( 1 ; + ∞ ) =======================