Naszkicuj wykresy funkcji Jednorożec michał: 1.Naszkicuj wykresy funkcji :

	π
a)y=sin(2x +		)
	3

	π
b)y=3cos(2x −		)
	2

2.Naszkicuj wykresy funkcji : a)y=cosx*tgx wskazówka ustal najpierw dziedzinę funkcji

	π
W 1a) mam rozrysować najpierw sin2x ,a następnie przesunąć w lewo		? ,a jak rozrysować
	3

resztę to nie mam pojęcia. Proszę o pomoc.

Gray:

	π
a) ... = sin2(x+		) czyli sin2x przesunięty o wektor [−π/6,0].
	6

	π
b) ... = 3cos2(x−		), czyli 3cos2x przesunięty o ....
	4

	π
2a) ... = sinx dla x≠		+kπ, k∊Z.
	2

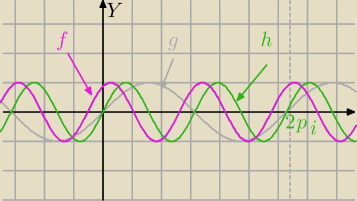Mila: a) Są dwa sposoby; wg Twojej kolejności powinno być tak: 1) g(x)=sinx 2)"Zagęszczenie" wykresu i otrzymujesz h(x)=sin(2x)

	π		π
3) Translacja o wektor [−		,0]=[−		,0]⇒
	2*3		6

	π
otrzymujesz wykres funkcji f(x)=sin(2x+		)
	3

	π
dlatego o		, że jeżeli przesuwamy wykres funkcji f(x) o wektor [a,b], to otrzymamy wykres
	6

funkcji o wzorze: f(x−a)+b więc w Twoim przykładzie y=sin(2x)po translacji o wektor

	π
u→=[−		,0] mamy:
	6

	π		π
f(x)=sin[2*(x+		)]=sin(2x+		) patrz rysunek
	6		3

II sposób (najpierw translacja ) 1)g(x)=sin(x)

	π		π
2) translacja o wektor [−		,0] ⇒h(x)=sin(x+		)
	3		3

	π
3) "Zagęszczenie" wykresu i otrzymujesz f(x)=sin(2x+		)
	3