... Hondziarz: Na paraboli o równaniu y= −x² − 2 wyznacz taki punkt P, aby styczna do tej paraboli poprowadzona w punkcie P ograniczała, wraz z prostymi o równaniach : x=0, y=0 , x=1. trapez o najmniejszym polu.

Hondziarz: Jak ktoś umie to proszę o pomoc.

Tadeusz: ... zrób rysunek i wszystko będzie jasne

Hondziarz: Zrobiłem i nic nie widze. Mam dwa miejsca zerowe, wierzchołek paraboli jest na prostej x=1, ... Ale co mi to daje?

O:: a jakie masz m₀?

Hondziarz: co to jest m₀?

O:: miejsce zerowe

Hondziarz: aa no to 0 i 2

O:: a to ciekawe, bo −0²−2≠0 i −2²−2≠0 czy sie mylę

Hondziarz: Ach Sory Źle przepisałem. Tam jest y= −x² − 2x Reszta bez zmian

Hondziarz: Jednak nie! y= −x² + 2x

Hondziarz: Tak to o 16:19 to wersja ostateczna

Tadeusz: ... to pojechałeś po całości −

O:: mam juz dość tego zadania. myśle i myslę ...

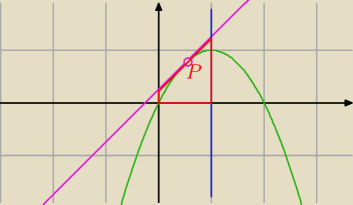
Tadeusz: Trapez ma wysokość 1 a jego pole będzie najmniejsze kiedy suma długości jego podstaw jest najmniejsza. Jeśli wyznaczymy równanie stycznej jako g(x) to sumę podstaw wyliczymy jako g(0)+g(1) i teraz: Punkt P=(x_p, −x_p²+2x_p) Równanie pęku prostych przez ten punkt: y+x_p²−2x_p=a(x−x_p) y=−x²+2x y'=−2x+2 y'(x_p)=−2x_p+2 podstawmy to w miejsce a y+x_p²−2x_p=(−2x_p+2)(x−x_p) y=g(x)=x_p²−2xx_p+2x g(0)+g(1)=x_p²+x_p²−2x_p+2=2x_p²−2x_p+2

	1
minimum dla xpw=
	2

	1		3
zatem P=(		,		)
	2		4

Tadeusz: ... ale nie sądzę aby to było zdanko na maturę −