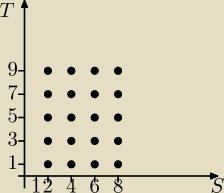
Relacje Le' the: Jako, że nie miałem wcześniej relacji, nie wiem za bardzo jak się za nie zabrać. Najpierw proste zadania, które rozumiem z relacji : ). Taką mam nadzieję. I.Niech S={2,4,6,8} oraz T={1,3,5,7,9}. Wypisz pary należące do relacji R⊂ S x T 1.x,y∈R⇔x+y <11 2.x,y∈R⇔x+y= 12 3.x,y∈R⇔x−y jest parzyste Najpierw rysujemy jak to wygląda w układzie współrzędnych. Teraz zaznaczamy odpowiednie punkty spełniające podanie nierówności. II. Które z własności spełnia dana relacja? zwrotność, przeciwzwrotność, symetria,przeciwsymetria, antysymetria, przechodniość x,y∈R,xρy⇔|x−y|<1; − wartość bezwzględna różnicy x i y ma być mniejsza od 1. Nie wiem jak to narysować. Poprzedni przykład był banalnym ten już nie jest.

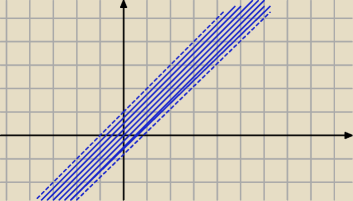
Le' the: Już wiem jak to narysować. Wychodzi taki. Ale co z tymi cechami? Pomożecie?

Le' the: x,y∈R,xρy⇔|x−y|<1 ktoś wie jakie cechy ma ta relacja? Wykres narysowany powyżej. A ich rodzaje są np tutaj: http://www.math.edu.pl/rodzaje-relacji Pomimo tego nadal nie wiem jakie są jej cechy.

Le' the: Może ktoś pomóc w określeniu cech tej relacji? Jak dla mnie: relacja jest zwrotna, symetryczna, przechodnia. Może ktoś sprawdzić?

Le' the: Może ktoś to sprawdzić?

PW: S={2,4,6,8} oraz T={1,3,5,7,9}. Zastrzegam, ze rozumiem zadanie w ten sposób, że relacja R jest podzbiorem iloczynu kartezjańskiego S×T, a zadanie ma trzy wersja (trzy różne relacje R). Przy takim rozumieniu ten "wykres" z 12:00 jest zły. Do zadania 1. relacja R to zbiór złożony z następujących par: (2, 7) (bo 1+9 < 11 (2, 5) (2, 3) (2, 1) (4, 5), (4, 3), (4, 1) (6, 3), (6, 1) (8, 1) (bo 8+1 < 11). Relacja nie jest zwrotna z tego powodu, że nie należy do niej żadna para (x, x) (a definicja mówi: dla każdej x musiałoby być (x, x)∊R). Z tych samych powodów relacja nie jest symetryczna (a wręcz przeciwnie − jeżeli (a, b)∊R, to (b, a) nie należy do R. Paradoksalnie można powiedzieć, że relacja R jest przechodnia, choć kłóci się to ze zdrowym rozsądkiem. Zdanie " jeżeli (a, b)∊R i (b, c)∊R, to (a, c)∊R" jest zdaniem prawdziwym jako implikacja o fałszywym poprzedniku (nie ma par (a, b) i (b, c) spełniających jednocześnie relację R).

Le' the: PW: Dziękuję za pomoc. Rozumiem już w jakimś stopniu relacje. Mam jeszcze kilka innych pytań. Mógłby ktoś odpowiedzieć? Czy istnieje inna metoda wyznaczania klucza prywatnego RSA niż rozszerzony euklides? To znaczy wyznaczanie odwrotności multiplikatywnej. Mam nadzieję, że nie mylę pojęć. Jak stosować chińskie twierdzenie o resztach? Miałem jakiś przykład z małymi wartościami w tabelce, ale zupełnie się on nie sprawdzi dla większych wartości. Jak rozwiązać np: x≡1 mod 3, x≡5 mod 11, x≡4 mod 25.

Le' the: Rysunek z 12:00 jest do x,y∈R,xρy⇔|x−y|<1. Jest zły?

Le' the: Ktoś pomoże z chińskim twierdzeniem w poście z 19:02?

PW: Zły, przecież nie "kawałek płaszczyzny", tylko wybrane punkty z tych, które narysowałeś o 11:52 (tam jest cały iloczyn kartezjański S×T, a każda relacja musi być jego podzbiorem).

Le' the: Źle to zapisałem. Ten podpunkt do którego jest wykres o 12 nie dotyczy już tego zadania co było wcześniej. Dane jest tylko: Które własności (zwrotność, przeciwzwrotność, symetria, przeciwsymetria, antysyme− tria, przechodniość) posiada dana relacja? I wymienione kilka relacji: ... x,y∈R,xρy⇔|x−y|<1 ...

Le' the: Jest jeden przykład którego nie rozumiem. Inne są podobne do tego co było wcześniej. A,B∈R,AρB⇔A⊂B − nie ma nic więcej powiedziane. Mam zbadać cechy tej relacji.

Saizou : mamy relację ApB ⇔ A⊂B mamy tak określoną relację no i sprawdzasz, łączność, symetrie, antysymetrie itp.

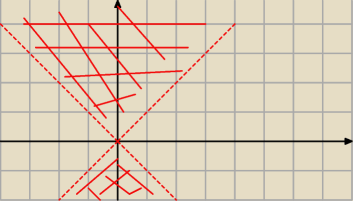
Le' the: Wcześniej było tak, że rysowałem sobie w układzie współrzędnych. Np jak było |x|<|y| to rysunek mniej więcej taki. I z rysunku mogę określić czy jest zwrotna czy nie. A jak mam narysować A⊂B?

Le' the: Ok. Czy A,B∈R,AρB⇔A⊂B będzie tak: Relacja zwrotna i symetryczna. Nie jest relacją przeciwzwrotną przeciwsymetryczną antysymetryczną