Rachunek różniczkowy. Blue: Mam do sprawdzenia 4 zadania dowodowe

	x2
zad.1 Dana jest funkcja f(x) =		. Wykaż, że równanie f '(x) = f(x) ma tylko jedno
	2x−2

rozwiązanie. http://i59.tinypic.com/sl2qo9.jpg http://i61.tinypic.com/qs79z6.jpg

	4
zad.2 Wykaż, że dla każdego m≥		funkcja f(x) = −x3 +2x2−mx−5 jest malejąca w zbiorze
	3

liczb rzeczywistych. http://i57.tinypic.com/2ic623l.jpg zad.3 Wykaż, że funkcja f(x) = x³ −2x² +8x−15 ma tylko jedno miejsce zerowe. http://i61.tinypic.com/oi50td.jpg zad.4 Udowodnij, że styczna do paraboli y=ax² w punkcie (x₀,y₀) przecina oś OY w punkcie (0,−y₀). http://i61.tinypic.com/54epk.jpg Proszę o ocenę I jeszcze jedno zadanko: W trójkącie ABC wierzchołek C leży na wykresie funkcji f(x) = √x oraz A=(−1,0) i B=(0,1). Wyznacz współrzędne punktu C tak, aby pole trójkąta ABC było najmniejsze. Zrobiłam to tak, że wyliczyłam odległość punktu C=(x,√x) od prostej AB i teraz liczyłam pochodną (w dwóch przypadkach, bo wartość bezwzględna) i wyszło mi w obu przypadkach m. zerowe

	1		1		1		1		−1
		. I wyszły z tego punkty (		,		) i (		,		), ale tę drugą opcję
	4		4		2		4		2

odrzucam , tak

Mila: 1) Dobrze. Można z mniejszą liczba rachunków.

Mila:

	2
2) Zbadaj kiedy f'(		)≤0
	3

3)f(x) = x³ −2x² +8x−15 ma tylko jedno miejsce zerowe, f(x) − funkcja ciągła f(0)=−15<0 f(2)=8−8+16−15=1>0 f'(x)=3x²−4x+8 Δ=16−4*3*8<0⇔f'(x)>0 dla każdego x∊R⇔f(x) jest funkcją rosnącą ⇔f(x) posiada jedno miejsce zerowe x₀∊(0,2) tw. Darboux

Mila: 4) Dobrze.

Mila:

	1
5) pole Δ=		|AB|*h
	2

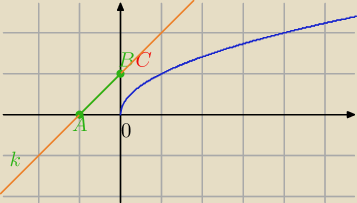
A=(−1,0) i B=(0,1) Najmniesze pole otrzymamy dla najmniejszej wartości h_AB, gdy C∊wykresu C=(x,√x) AB: y=x+1⇔x−y+1=0

	|x−√x+1|
d(C,k)=
	√2

dla x>0 (bo x≥√x)

	2√x−1
d'(x)=		, x≠0
	2√2√x

	1		1		1
d'(x)=0⇔x=		i d'(x)>0 dla x>		⇔d(x) ma min. w punkcie x=
	4		4		4

	1		1   1   − +1 4   2		3		3√2
d(		)=		=		=
	4		√2		4√2		8

Badamy d(0) w punkcie x=0 bo tam nie ma pochodnej, ale może byc wartość najmniejsza d(x)

	1		√2
d(0)=		=
	√2		2

	3√2		√2
Posprawdzaj rachunki i porównaj		i		a następnie odp.
	8		2

Blue: Czyli Mila, to moje rozwiązanie 2 jest niepoprawne Nie było by takie coś zaliczone?

Blue: To samo pytanie tyczy się 3 zadania... Mi się wydaje, że udowodniłam, że ta funkcja jest rosnąca w zbiorze l. rzeczywistych

razor: w 3 udowodniłaś że funkcja jest rosnąca, ale nie że ma miejsce zerowe − np. 2^x jest rosnąca a nie ma miejsca zerowego

Blue: Mila, nie ogarniam za bardzo tego liczenia d(0) po co my to robimy?

Blue: aaa ok, bo muszę jeszcze pokazać, że gdzieś są wartości na plusie, a gdzieś na minusie, tak razor?

Blue:

	3√2
ale w tym 5 nawet jeśli już dojdziemy do tego, że		jest mniejsze, to jak podstawimy
	8

	1
do współrzędnych punktu C		, to nam wyjdą dwa rozwiązania. Ale to jedno odrzucamy tak na
	4

	1
oko, bo widać, że		będzie bliżej , tak
	2

razor: tak

razor: odpowiadam do 14:40

Blue: ok

razor: ewentualnie jak nie możesz znaleźć takich wartości dla których wartości funkcji są ujemne lub dodatnie możesz pokazać że lim_x−>∞ f(x) = ∞ i lim_{x−>− ∞} f(x) = −∞

Blue: też dobry sposób, dzięki

Kacper:

Blue: Kacper może pomożesz?

Lukas: Ja Ci pomogę

Mila: Nie wiem w czym masz problem. Masz dać odp.

	1		1
C=(		,		)
	4		2

Blue: Dobra, nieważne, dzięki Mila za pomoc