Geometria :) Blue: Mam do sprawdzenia 2 zadania na dowodzenie: zad.1 Udowodnij, że trójkąt o wierzchołkach A=(0,0), B−(a,b), C=(−b,a) jest trójkątem prostokątnym:

	1
zad.2 Uzasadnij, że każdy punkt paraboli y=		x2 jest oddalony od prostej x−2y−10=0 co
	4

najmniej o 2√5. Moje rozwiązania: http://i62.tinypic.com/2hzo3s7.jpg http://i58.tinypic.com/28ip168.jpg − Dopiero teraz zauważyłam, że do zadania 2 rysunek jest źle zrobiony, ale to nieistotne zad.3 Wyznacz wszystkie wartości parametru m, dla których prosta o równaniu 2x−3y+m = 0 ma jeden punkt wspólny z odcinkiem o końcach A=(1,2) i B=(−1,4). DOBRZE MI TO WYSZŁO, WIĘC NIE LICZCIE TEGO Tylko chce się dowiedzieć, czy mój sposób rozwiązania jest poprawny Ja robiłam to tak: Wiadomo, że prosta ta ma współczynnik

	2
kierunkowy		i skoro to wiemy, to możemy wyznaczyć b, kiedy prosta ta przechodzi przez
	3

punkt A i przez punkt B. Będziemy mieli tym samym minimalną wartość b i maksymalną wartość b

	m
, a że b =		, to m już łatwo wyliczyłam
	3

Blue: hm.... to drugie chyba jednak źle zrobiłam

O:: 1. dobrze

Blue: a 2?

Tadeusz: do 2) Poszukaj prostej równoległej do danej prostej mającej z parabolą jeden punkt wspólny

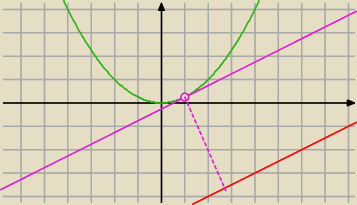
Tadeusz: czyli: x/2+b=x²/4 ⇒ x²−2x−4b=0 Δ=4+16b Δ=0 b=−1/4 wtedy (x−1)²=0 x_o=1 y_o=1/4 . to są współrzędne punktu położonego najbliżej itd ...

Tadeusz: ... chyba, że wolisz z pochodną −

Mila: W pierwszym możesz wykorzystać Pitagorasa.

Blue: ale Tadeusz z tego wynika, że najbliżej położony punkt jest oddalony o 1,9√5... Czyli moje rozwiązanie zad, 2 jest złe Znalazłam też takie rozwiązanie: http://forum.zadania.info/viewtopic.php?t=66150&p=247480

Tadeusz: ... to pierwsze rozwiązanie daje wynik identyczny z moim

Tadeusz:

	9,5√5
...punkt położony najbliżej prostej oddalony jest od niej o
	5

Mila: Blue, zadanie 2 masz źle zrobione .

	1
Ja badałabym odległość P(x,		x2)∊paraboli od prostej x−2y−10=0.
	4

Czy masz z tym problem?

Tadeusz: ...drugie rozwiązanie z Twego linku jest absurdalne bo zakłada, że najbliżej położonym punktem jest wierzchołek paraboli.

Tadeusz: ...tyle, że teza postawiona w zadaniu jest nie prawdziwa

Tadeusz: ... Eta ... zerknij proszę na to zadanko. Co sądzisz o tezie postawionej w zadaniu?

Blue:

	9,5√5
no właśnie Tadeusz o to mi chodzi, że przecież		jest przecież mniejsze od
	5

2√5...

Blue: Mila teraz już rozumiem, ale ta treść zadania mnie zmyla

Blue: Czyli mam rozumieć, że treść jest zła?

Tadeusz: a skąd jest to zadanie?

Tadeusz: ... jak dla mnie ...to zła. Ktoś układając zadanie założył, że najbliżej położonym jest wierzchołek paraboli.

Blue: haha, czyli tak jak pierwotnie ja xp Aksjomat. Mila, a Ty co sądzisz

Mila: Tak samo. d_min=1.9√5 Rozwiązywałam inaczej niż Tadeusz, to samo wychodzi. Nie martw się na maturze nie będzie odpowiedzi, a rozwiązania będą sprawdzane jak należy.

Martiminiano: Blue, pisałem do Ciebie maila.

Blue: ok, zaraz zajrzę, ogólnie rzadko na niego wchodzę, więc sorki, że nie odpowiadałam