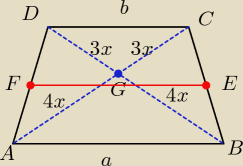
podobno trzeba wykorzystać podobieństwo trójkątów sapiens w potrzebie: Takiego zadania chyba jeszcze nie było Przekątne trapezu dzielą sie w stosunku 3:4 . Odcinek łączący środki jego ramion ma dł. 14. obilcz długość dłuższej podstawy trapezu

Eta: He,he..... Może i nie było ,bo jest łatwe... ΔDGC ~ ΔAGB w skali k= ³₄ to:

	b		3
		=		to => b= 34*a
	a		4

	a+b
linia środkowa trapezu IEFI=		= 14
	2

to a+b = 28 to a + ³₄a = 28 => ⁷₄*a= 28 => a= 28*⁴₇= 16 dolna podstawa ma długość a= 16 górna podstawa b = ³₄*16= 12 odp: a=16

Basia: Eto, czy to musi być trapez równoramienny ? Nie wydaje mi się.

Bogdan: Przekątne tego trapezu mają długość 7x, a więc są równej długości. Które trapezy mają przekątne równej długości ?

Eta: Witam Bogdanie Basia chyba zmęczona była?

Bogdan: Dzień dobry Eto

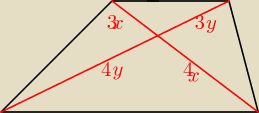
Basia: Wcale nie muszą mieć 7x. Mogą mieć 7x i 7y. Skąd wiadomo, że x=y ? Całkiem możliwe, że tak jest, ale skąd to wiadomo ?

Basia: Nawiasem mówiąc to nie ma wpływu na rozwiązanie tr.ASB ∼ tr.CSD w skali s=⁴₃ stąd: a=⁴₃b

a+b
	= 14
2

a+b = 28 ⁴₃b+b = 38 4b+3b=28*3 7b=28*3 b = 4*3 = 12 a=⁴₃*12 = 16

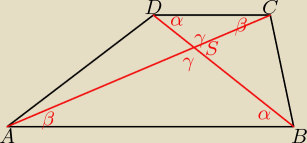
Basia: I kto tu był zmęczony ? W każdy trapezie przekątne dzielą się w stosunku ^a_b, co wynika oczywiście z tego, że tr.ASB i tr.CSD zawsze są podobne (bo mają takie same kąty) Stąd:

AS		BS		AB		a
	=		=		=
CS		DS		CD		b

to jak najbardziej może być 4:3 i nikt mi nie wmówi, że z treści zadania wynika, że jest to trapez równoramienny. AS=4x CS=3x BS=4y DS=3y warunki zadania są spełnione.

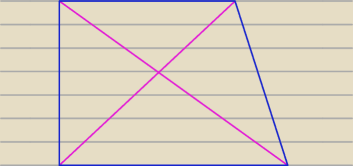
Bogdan: Dzień dobry. Na tym rysunku przekątne trapezu dzielą się w stosunku 3: 4, ale ten trapez nie jest równoramienny.

sapiens w potrzebie: Basiu dlaczego 4/3b+b ? ( nie wiem jak tu sie pisze ułamki)

sapiens w potrzebie: Basiu dlaczego 4/3b+b ? ( nie wiem jak tu sie pisze ułamki)

sapiens w potrzebie: i skąd wzór a+b/2 = 14 (14 to wiem że to jest ta kreska po środku)

Basia: Witaj sapiens. Wybacz, że dopiero teraz, ale dwa dni mnie tu niestety nie było. 1. Z lewej strony masz link "Kliknij po więcej przykładów". Tam przeczytasz jak pisać ułamki. 2. Ponieważ ^a_b = ⁴₃ co wynika z podobieństwa trójkątów mnożymy przez b (oczywiście obustronnie) ^a_b*b = ⁴₃*b a = ⁴₃b 3. ^a+b₂ = 14 to wynika z tw.Talesa mnożysz przez 2 a+b = 28 podstawiasz za a ⁴₃*b + b = 28 /*3 4b+3b=3*28 7b=3*28 /:7 b=^3*28₇ = 3*4 =12