Prosze o pomoc
Ona: Zaznacz na układzie współrzędnych obszar określoności funkcji:
f(x,y)=
√x2+y2−1+
√4−x2−y2
| df | | 1 | | 1 | |
| =(√x2+y2−1+√4−x2−y2)`= |
| (x2+y2−1)`+ |
| |
| dx | | 2√x2+y2−1 | | 2√4−x2−y2 | |
| | x | | x | |
(4−x2−y2)`= |
| − |
| |
| | √x2+y2−1 | | √4−x2−y2 | |
| df | | 1 | | 1 | |
| = |
| (x2+y2−1)`+ |
| (4−x2−y2)`= |
| dy | | 2√x2+y2−1 | | 2√4−x2−y2 | |
Obliczyłam pochodne cząstkowe (przepraszam że tak po łebkach ale strasznie dużo pisania), ale
nie wiem co dalej musze zrobić

Pomożecie ?
11 gru 10:20
J:
..wydaje mi się,że nie o to tu chodziło ... masz w ukladzie współrzędnych zaznaczyć obszar
określoności funkcji, czyli innymi słowy dziedzinę tej funkcji ...
11 gru 10:22
Ona: Jak mam to zrobić, bo nie wiem ?
11 gru 10:32
J:
x2 + y2 − 1 ≥ 0 i 4 − x2 − y2 ≥ 0 ...
11 gru 10:38
Ona: Układ równań?
11 gru 10:41
J: ..nie rozwiązuj tego układu .. po po co ?
.. pierwsza nierówność do zewnetrze okręgu o środku S(0,0) i promieniu r = 1
druga , to wnetrze okręgu o środku S1(0,0) i promieniu r = 2 .
część wspólna to wnętrze pierściena: S(0,0} r1 = 1 , r2 = 2 ... i narysuj ...
11 gru 10:46
Ona:
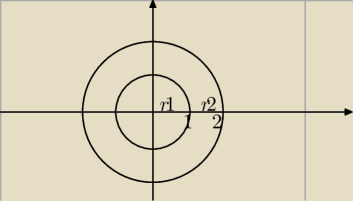
Tak?
11 gru 10:58
J:
... i teraz zakreskuj wnętrze ...bez okręgów , bo nierówności są "słabe" ...
11 gru 11:01
11 gru 11:06
J:
zaznaczyłaś wnętrze okręgu S(0,0) i r = 2 , a masz zaznaczyć wnętrze pierścienia, czyli bez
okręgu S(0,0) i r = 1
11 gru 11:13
abc: Aha rozumiem

Moge podać jeszcze jeden przykład, bo nie rozumiem do końca jak to się robi

?
11 gru 11:15
 Pomożecie ?
Pomożecie ?
 Tak?
Tak?
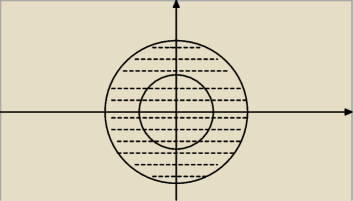 Tak
Tak 

 Moge podać jeszcze jeden przykład, bo nie rozumiem do końca jak to się robi
Moge podać jeszcze jeden przykład, bo nie rozumiem do końca jak to się robi ?
?