funkcja liniowa, przekształcanie wykresów Nana: Nie rozumiem czemu tak jest w odpowiedziach... Mamy funkcję f(x) której wykres zawiera punkty A=(0,0) i B=(4,2). z tego wynika, że funkcja ma wzór y=¹₂x. Jak się nie pomyliłam gdzieś już na tym etapie. Mam naszkicować wykres funkcji g(x)=f(x−2), czyli jak im wyszło, że g(x)=¹₂x−1 i jaki wzór ma funkcja g(x)=f(x)+3? Jaka jest różnica w tym, czy liczba jest w nawiasie czy nie? Proszę o wytłumaczenie tego.

daras: a jak ci wyjdzi e, ż ewzór jest f(xg(y)) to czy to oznaczaze punkt (0, 0) nalezy do wykresu? czy jest może to wykres przesunięty o wektor [3,2] w stosunku bez..?

PW: f(x−2) oznacza utworzenie funkcji, która ma takie same wartości jak f, ale osiągane w innych punktach − co oznacza przesuniecie wykresu funkcji f w prawo o 2. Funkcja f(x) + 3 osiąga wartości o 3 większe niż f(x), ale dla tych samych x, co oznacza przesunięcie wykresu o 3 w górę.

Nana: wykres f(x) jest narysowany już w zadaniu. Odczytałam z wykresu punkt A i B, żeby podać wzór tej funkcji. I teraz nie wiem jak mam przekształcić ten wykres żeby g(x)=f(x−2) i g(x)=f(x)+3

Janek191: A = ( 0 ; 0) B = ( 4; 2) więc

	1
y =		x
	2

	1		1
g(x) = f( x − 2) =		*( x − 2) =		x − 1
	2		2

więc wykres funkcji f przesuwamy o wektor [ 2 ; 0 ] oraz

	1
h(x) = f(x) + 3 =		x + 3
	2

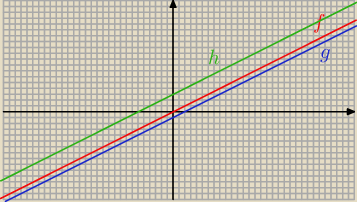
więc wykres funkcji f przesuwamy o wektor [ 0 ; 3 ] Dodatkowo − wykresy: