Kąty między prostą a płaszczyzną i kąt dwuścienny
rak: Poproszę TYLKO o rysunki.
1. Trzy punkty A,B,C leżące na płaszczyźnie π wyznaczają trójkąt równoramienny, w którym
AC=BC=5 oraz AB=6. Odcinek DC jest prostopadły do płaszczyzny π, a jego długość równa się 8.
Oblicz:
a) tangens kąta nachylenia prostej BD do płaszczyzny π
b) tangens kąta nachylenia płaszczyzny (ABD) do płaszczyzny π
2. Trójkąt prostokątny ABC zawiera się w płaszcyźnie π przy czym |∠ABC|=90o oraz AC=20, AB=12.
Odcinek DC jest prostopadły do płaszczyzny π i ma długość 12. Oblicz:
a)sinus kąta nachylenia prostej AD do płaszczyzny π
b) sinus kata nachylenia płaszczyzny (ABD) do płaszczyzny π
10 gru 18:30
M:
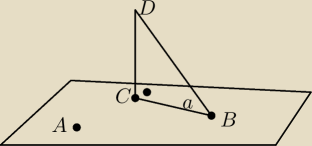
1a)
10 gru 18:38
M:
b)DC prostopadłe do CE
10 gru 18:43
M: z drugim sobie poradzisz, tak samo narysuj
10 gru 18:44
rak: Dzięki.
Teraz zobaczę czy mi wyjdzie.
10 gru 18:46
rak: W 1a przy kącie c jest kąt prosty?
10 gru 18:50
M: tak CD jest prostopadłe do wszystkich prostych na π
10 gru 18:52
rak: Czyli trójkąt DCB jest prostokątny i ACD też?
10 gru 18:54
rak: I skąd wzięte E?
10 gru 19:02
M: EC − wysokość trójkąta ABC i tak prostokatne
10 gru 19:56
M: DE − wysokość trójkąta ABD
10 gru 19:56