geometria analityczna Kuba: Mamy dane wierzchołki trójkąta A(3, 1) B(1, −3). Środek ciężkości tego trójkąta należy do osi OX, a pole wynosi 3. Wyznacz współrzędne trzeciego wierzchołka. Mam już jedno równanie z dwoma niewiadomymi wykorzystując wzór na pole z użyciem wektorów, nie wiem jak wykorzystać dane o środku ciężkości

Kuba:

Mila:

	xA+xB+xC
xs=
	3

	yA+yB+yc
ys=		w tym zadaniu ys=0⇔
	3

1−3+yc
	=0⇔yc=2⇔punkt C leży na prostej y=2
3

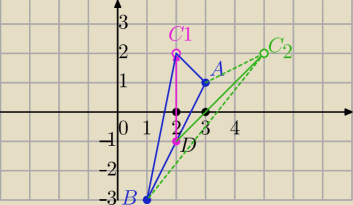
Mila: A(3, 1) B(1, −3),C=(x_c,y_c) S=(x₀,0)− wsp. środka ciężkości ( punkt przecięcia środkowych Δ)

	xA+xB+xC
x0=
	3

	yA+yB+yC
0=
	3

⇔

	3+1+xC
x0=		⇔3x0=xc+4⇔xC=3x0−4
	3

	1−3+yC
0=		⇔yc=2
	3

Dołącz do równania z wzoru na pole. Napisz, czy taka odpowiedź jak masz na rysunku.