fizyka
kyrtap: Potrzebuję fizyka

9 gru 23:25
Metis: Może
Daras sie pojawi, może
MQ
Napisz to przeczytają

9 gru 23:27
kyrtap: Wyjaśnić czy pole sił F→ będące sumą dwóch pól sił potencjalnych F1→, F2→ jest potencjalne
:
a) na podstawie definicji(całka po dowolnej krzywej zamkniętej)
b) na podstawie kryterium rot F→ = 0
9 gru 23:29
MQ:
Ad a)
F→=F1→+F2→
∫F→dr→=∫(F1→+F2→)dr→=∫F1dr→+∫F2dr→
A ponieważ F1→ oraz F2→ są polami potencjalnymi, więc:
∫F1dr→=0 i ∫F2dr→=0
stąd:
∫F→dr→=0
oczywiście całkuję po konturze zamkniętym −− tutaj się nie da tego napisać
Ad b)
Rotacja jest operatorem liniowym, więc:
rot(F1→+F2→)=rotF1→ + rotF2→
dalsze rozumowanie, jak wyżej
9 gru 23:41
kyrtap: po konturze zamkniętym co to oznacza

9 gru 23:45
MQ: No, właściwie, to po krzywej zamkniętej. Przejęzyczyłem się.
9 gru 23:47
kyrtap: i to jest całka oznaczona

9 gru 23:48
kyrtap: moje zaliczenie kolokwium z fizyki graniczy z cudem −.−
9 gru 23:53
MQ: Można ją zapisać w postaci całki oznaczonej, ale zapisuje się ją raczej symbolem znaku całki z
nałożonym kółeczkiem na środku i pod spodem oznaczenie konturu (zazwyczaj duża litera C).
9 gru 23:55
kyrtap: MQ pomożesz jeszcze z jednym zadaniem

bo jeszcze jedno zostało z którym mam problem
9 gru 23:56
kyrtap: a można tylko ten znak falbanki i tyle tak?
9 gru 23:56
MQ: Jakiej falbanki?
9 gru 23:57
MQ:
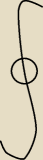
Tak zazwyczaj pisze się znak całki po konturze zamkniętym.
9 gru 23:58
kyrtap: nie wiem bo tylko miałem całkę oznaczoną na fizyce ale dzięki MQ że pokazałeś jak to wygląda

9 gru 23:59
kyrtap: MQ dasz radę jeszcze z jednym zadankiem

10 gru 00:03
MQ: Nie wiem, jeszcze go nie widziałem. Wrzucaj.
10 gru 00:04
kyrtap: Tytuł zadania: Energia potencjalna i siła
Energia potencjalna punktu materialnego w pewnym polu sił wynosi Ep(x,y,z) = x2 + y2z + xyz
a) znaleźć odpowiadające jej pole sił
b) Wyznaczyć pracę potrzebną na przeniesienie rozważanego punktu materialnego z punktu A(0,0,0)
do punktu B(1,1,1)
10 gru 00:08
MQ: Pole sił liczysz z gradientu energii potencjalnej (zauważ, że tam jest minus przed gradientem):
F(r)
→=−gradE(r)
czyli masz:
| | dE | | dE | | dE | |
F(r)→= |
| i→+ |
| j→+ |
| k→ |
| | dx | | dy | | dz | |
Tam powinny być pochodne cząstkowe, ale tu nie ma tych znaczków, więc dałem d.
i,j,k to oczywiście wersory.
U ciebie wychodzi:
F
→=(2x+xy)i
→+(2yz+xz)j
→+(y
2+xy)k
→
A pracę liczysz jako całkę oznaczoną:
∫F
→dr
→, w granicach od A do B.
Pod całką masz iloczyn skalarny:
F
→dr
→=(2x+xy)dx+(2yz+xz)dy+(y
2+xy)dz
10 gru 00:22
kyrtap: moje dni są policzone chyba jeśli chodzi o fizykę dzięki wielkie jeszcze raz MQ
10 gru 00:24
MQ: Fizyki w tym tyle, co kot napłakał −− praktycznie czysta matematyka.
10 gru 00:32
kyrtap: fajnie że to miałem na matmie dopiero pierwszy semestr a już jakieś gradienty mam

10 gru 00:36
kyrtap: będę musiał do tego przysiąść i poczytać sporo o tym
10 gru 00:42
10 gru 00:43
kyrtap: Dzięki MQ że pomogłeś przynajmniej wiem czego nie umiem
10 gru 00:45
MQ: W zasadzie, to tę pracę nie trzeba liczyć całką, bo mamy pole potencjalne, więc praca przejścia
z punktu A do B to różnica energii potencjalnych w tych punktach, a wzór na Ep mamy dany.
10 gru 09:03




 bo jeszcze jedno zostało z którym mam problem
bo jeszcze jedno zostało z którym mam problem
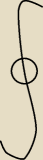 Tak zazwyczaj pisze się znak całki po konturze zamkniętym.
Tak zazwyczaj pisze się znak całki po konturze zamkniętym.


