geometria Blue: zad.8 Na płaszczyźnie dane są cztery punkty A=(1,2), B=(5,4), C=(3,6), D=(0,8). Przez punkt D poprowadzono prostą l prostopadłą do prostej AB. Znajdź na prostej l taki punkt E, aby pole trójkąta ABC było równe polu trójkąta ABE. Problem polega na tym, że coś mi nie wychodzi Umiem to liczyć (tak mi się wydaje), ale delta mi nie wychodzi ;c

	1		3
Robię tak: prosta l: y=−2x+8, AB: y=		x+		i teraz liczę wysokość trójkąta ABC
	2		2

(odległość punktu C od prostej AB), potem liczę punkt przecięcia prostych i teraz wiem, że odległość tego punktu od punktu E musi być równa wysokości, która mi wyszła... i liczę to ze wzoru na odległość punktów i mi nie wychodzi :C Pomocy

Blue: Jakby co, to już się doliczyłam Po prostu liczby były trochę nieprzyjemne i popełniłam błędy rachunkowe

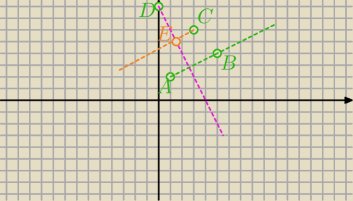Tadeusz: oczywiście można znacznie prościej − Ta sama podstawa trójkątów więc i wysokości muszą być równe. Wniosek taki, że punkty C jak i E leżą na prostej równoległej do prostej przez A i B.

Mila: To dobrze. Chyba zbyt skomplikowany wybrałaś sposób. Trzeba skorzystać ze wzoru na odległość punktu C=(3,6) od prostej x−2y+3=0 i porównać z odległością punktu E=(x_e,−2x_e+8) od tej prostej.

|1*3−2*6+3|		|1*xe−2*(−2xe+8)+3|
	=
√1+22		√5

Otrzymałaś dwa rozwiązania?

Blue: tak