Zespolone....
xdx: Wytłumaczył by mi ktoś przykład z liczb zespolonych. Mam zaznaczyć na płaszczyznie
Im((2 + 4i)z − 2i) > Re(4), Czyli rozumiem Re(4)=4..
A w tym Im nie wiem co z tym z
9 gru 20:56
Marcin: Im, to część urojona liczby zespolonej.
9 gru 20:57
xdx: To wiem ale mam Im((2 + 4i)z − 2i) i przez ten z mam najpierw pomnożyć
9 gru 20:58
Marcin:
(2+4i)z−2i=
2z+4iz−2i=
2z+(4z−2)i
Więc Im(2z+(4z−2)i)=4z−2

9 gru 21:00
Gray: Oj. Zwykle z to liczba zespolona...
9 gru 21:01
xdx: ok To teraz muszę zaznaczyć 4z−2>4
9 gru 21:04
kyrtap: Marcin no co ty nie powiesz?

9 gru 21:05
Mila:
z=x+iy, x,y∊R
(2 + 4i)z − 2i) =(2+4i)*(x+iy)−2i=
=2x+2iy+4xi−4y−2i=(2x−4y)+i*(2y+4x−2)
Im[(2x−4y)+i*(2y+4x−2)]=2y+4x−2
2y+4x−2>4⇔
2y>−4x+6
y>−2x+3 punkty nad prostą y=−2x+3
9 gru 21:08
Marcin: Racja, potwierdzam.
9 gru 21:10
xdx: Ok dzięki Mam jeszcze jeden przykład |2z − 4| ≥ 3, tutaj z0=4
A 2 mogę wyciągnąć z wartości bezwzględnej przy z?
9 gru 21:12
kyrtap: I2z−4I≥3
I2I Iz−2I ≥3 /:2
9 gru 21:13
Mila:
Możesz :
|2z−4|≥3 /:2
| | 3 | | 3 | |
|z−2|≥ |
| punkty poza kołem o środku (2,0) i r= |
| |
| | 2 | | 2 | |
9 gru 21:14
xdx: No tak i zaznaczę teraz z0=2 rysuję koło o promieniu 3/2
9 gru 21:15
xdx: To już to powoli rozumiem a jak mam taki przykład to
π/3≤ 2 · arg(z) < 2π to dzielę na 2 i mam
π/6≤ arg(z) < π i rysuję kąt?
9 gru 21:17
xdx: Możecie powiedzieć czy w poprzednim poście mam dobrze i mam jeszcze pytanie do postaci
wykładniczej mam przykład z4 = eπ i mam wyznaczyć argument i moduł ale nie ma i w potędze e
9 gru 21:33
Mila:
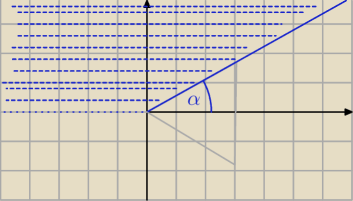
9 gru 21:51
xdx: Ok. Czyli dobrze rozumiałem a te moje pytanie o postać wykładniczą
9 gru 21:59
Gray: z=eπ to liczba rzeczywista dodatnia, więc |z|=eπ, argeπ=2kπ, k∊Z.
9 gru 22:00
xdx: A jak mam to zapisac w postaci trygonometrycznej to
z=eπ(cos2kπ + isin2kπ) tak?
9 gru 22:03
Gray: z=eπ(cos2kπ+ isin2kπ)
10 gru 08:28


