POMOCY !!! waszka: Punkty A=(2,0) i B=(12,0) sa wierzcholkami trojkata prostokatnego ABC o przeciwprostokatnej AB. Wierzcholek C lezy na prostej o rownainiu y=x. Oblicz wspolrzedne punktu C

Eta: To zad. z tegorocznej próbnej matury

waszka: dokladnie a pomozesz mi je zrobic bo jestem na humanie w 2 liceum i Pani od maty dala to zad jako dodatkowe ;\

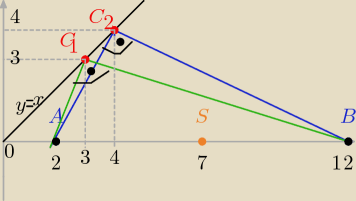
Eta: IABI= I12−2I= 10 ponieważ trójkąt ABC jest prostokątny to środek S okręgu opisanego na tym trójkącie jest środkiem przeciwprostokatnej AB

	xA+xB		yA+yB
zatem xS=		i yS=		i r= 12IABI
	2		2

więc S( 7,0) i r= 5 rozwiązując układ równań tego okręgu z proztą y=x otrzymamy C(x,y) równanie okręgu: ( x −7)² +(y−0)²= 25 x² −14x +49 +y² = 25 i y = x x² −14x +49 +x² =25 2x² −14x +24=0 => x² −7x +12=0 dokończ policz deltę i wyznacz x₁ i x₂ i następnie y₁ i y₂ odp: są dwa takie punkty spełniajace warunki zadania C₁( 3,3) C₂(4,4) co też widać na rysunku