równania prostych - zadania Nka: Dane są punkty A(1,0) oraz B(5,2). Na prostej k równoległej do prostej AB i przechodzącej przez punkt P(4,4) wyznacz współrzędne punktu C, który jest równoodległy od punktów A i B. Chciałabym to zrobić wykorzystując fakt, że prosta k i symetralna odcinka AB mają punkt wspólny → C. Zrobiłam tak: wektor AB=[4,2] k: 4*4+2*4+C=0 → k: 2x+y−12=0 środek odcinka AB: (3,1) i podstawiłam do wzoru: 4(x−3)+2(y−1)=0 → l: 2x+y−7=0 i aby znaleźć współrzędne punktu C zrobiłam tak: { 2x+y−7=0 {2x+y−12=0 I wszystko się skraca, więc proszę o pomoc co robię źle

Nka: pomoże ktoś?

kiko: skorzystaj z odległości

czarny: Już wuem, dzięki

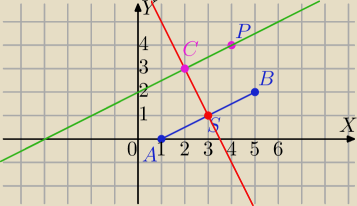
Mila: S=(3,1) AB^→[4,2] wektor równoległy do AB, wektor prostopadły do symetralnej: P(4,4)∊prostej p równoległej do AB s: 4x+2y+C=0 , aby wyznaczyc C podstawiamy wsp. punktu S 4*3+2*1+C=0⇔C=−14 s: 4x+2y−14 =0 /:2 2x+y−7=0 równanie symetralnej AB (y=−2x+7) Prosta p jest prostopadła do symetralnej [2, −4] wektor prostopadły do p 2(x−4)−4*(y−4)=0 ⇔ 2x−4y+8=0 równanie równoległej do AB ( prostopadłej do s)⇔

	1
p: y=		x+2
	2

po rozwiązaniu układu: 2x−4y+8=0 4x+2y−14 =0 C=(2,3)