Sprawdzicie Ona :

	1
Wyznacz monotoniczność i ekstrema lokalne funkcji y=x+
	x

1) Dx∊R/{0}

	1		(1)`(x)−(1)(x)`		1
2) y`=(x)`+(		)`=1+		=1−
	x		x2		x2

	1
3) 1−		=0 /*(x2)
	x2

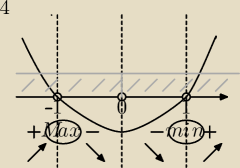
x²−1=0 x²=1 x=1 x=−1 4) Przybliżony wykres 5)f(x)↗(−∞,−1)u(1,∞) f(x)↘(−1,1) Fmax=f(−1)=−2 Funkcja osiąga max lokalne w pkt (−1,−2) Fmin=f(1)=2 F−cja osiąga min lokalna w pkt (1,2)

===:

===: ... czyli wszystko ok −

Ona : Jeżeli mam w poleceniu obliczyć monotoniczność i ekstrema f−cji to muszę liczyć max i min w punkcie tak jak to zrobiłam na końcu? Czy moge to pominąć ?

===: ... tylko w przedziale w którym funkcja maleje uwzględnij dziedzinę