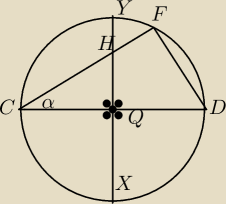
Dowód Metis: Wykaż, że α=30⁰, wiedząc że XY i CD to prostopadłe średnice. Cięciwa CF przecina srednice XY w takim punkcie H że w czworokąt QDFH możemy wpisać okrąg. Jakiś pomysł ? Oczywiście kąt przy wierzchołku F = 90⁰ Cały dowód byłby załatwiony gdybym pokazał że kąt przy D = 60⁰. Co mogę wycisnąć z informacji: "że w czworokąt QDFH możemy wpisać okrąg" ?

prymo96: "że w czworokąt QDFH możemy wpisać okrąg ". W czworokąt można wpisać okrąg ,wtedy gdy np: HF +QD = HQ + FD

prymo96: i z drugiej własności ,mowiacej ze: trójkąt oparty na średnicy jest zawsze prostokątny ,stąd przy F będzie 90

Metis: 1) "Wycisnąć" coś co pomoże mi w dowodzie... Zależność, którą podałeś znam Nie widzę związku tej zależności z moim zadaniem. 2) Napisałem ....

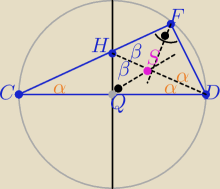
Eta: Środek okręgu wpisanego w czworokąt HFDQ znajduje się w punkcie przecięcia dwusiecznych kątów Dwa kąty czworokąta mają miary po 90^o to 2α+2β= 180^o ⇒ α+β= 90^o Trójkąt CHD jest równoramienny o ramionach |CH|=HD| to |∡DCF|=α zatem w trójkącie CDF 2α+α=90^o ⇒ α=30^o

Metis: Dziękuje serdecznie Eta Jak ty to wszystko widzisz

Metis: Eto jesteś

Eta: Jestem

b: Eta jest bogiem, uświadom to sobie

Metis: Powiedz mi czy ta informacja do momentu stwierdzenia ze jest to trójkąt rownoramienny jest konieczna ?

Eta: Tak, bo wtedy zauważamy trójkąty prostokątne przystające ΔHDQ≡ ΔHFD z cechy (kbk) ⇒ |DQ|=|FD| i |HF|=|HQ| teraz zuważ,że |CQ|=|QD|=R ⇒ Δ CHD równoramienny itd ............

Eta: Żyjesz Metis ?

Metis: Przepraszam Eta ale sen wziął górę Oczywiście rozumiem , ale myślałem nad tym aby napisać od razu , |CH|=|HD|

Metis: Dziękuję jeszcze raz