równania prostych

równania prostych ejej: Punkty A(2,−3) i B(5,1) są wierzchołkami trójkąta ABC. Bok BC zawiera się w prostej o równaniu k:x+2y−7=0, zaś środkowa AM zawiera się w prostej m: 5x−y−13=0. Wyznacz równanie ogólne prostej, w której zawiera się wysokość trójkąta poprowadzona z wierzchołka C.

7 gru 18:11

ejej: pomocy

8 gru 22:38

Eta:

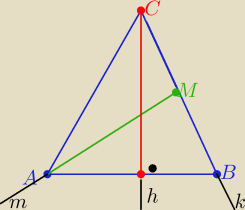
1/ rozwiąż układ równań danych prostymi k i m otrzymasz współrzędne punktu M(....,...) ,który jest środkiem odcinka BC 2/ ze wzoru na współrzędne środka odcinka: x_c= 2x_M−x_B i y_C= 2y_m−y_B C(....,....) 3 / prosta h ⊥ do prostej AB i C∊h

	y_A−y_B
wsp. kierunkowy a_AB=		=.......
	x_A−x_B

	1
wsp. a_h= −		=.....
	a_AB

prosta h: y= a_h(x−x_C)+y_C) ⇒ h=.......... teraz dokończ .........

8 gru 23:36

Eta: Ejejjjjjj emotka

jak tam?

8 gru 23:58

muuu: Niegrzeczny nick, niegrzeczne zachowanie.

9 gru 00:08

ejej: po prostu zasnąłem... zobaczę po południu, bo muszę już wychodzić, ale serdecznie dziękuję za pomoc emotka

9 gru 07:00

ejej: po przeanalizowaniu nie rozumiem od momentu pojawienia się współczynnika kierunkowego. Nie znam tego wzoru

9 gru 21:08

ejej: już wiem

DZIĘKUJĘ

9 gru 21:12

Eta:

9 gru 21:13