wykaż że następujące funkcje są ciągłe w zbiorze liczb rzeczywistych pcv: wykaż że następujące funkcje są ciągłe w zbiorze liczb rzeczywistych f(x) = x3 + 2 x2 − 5

M:

#k: Mówimy krótko : funkcja ciągła w przedziale domkniętym przybiera każdą wartość pośrednią między swymi wartościami na końcach przedziału f(x)=x³+2x²−5 Dla x=0 f(0)=−5 dla x=1 f(1)= 1+2−5= −2 Sprawdzmy więc czy dla pewnego x∊<0,1> funkcja przyjmie wartośc (−4) pośrednia miedzy (−5) i (−2) x³+2x²−5=−4

	1
Dla x=U{√5}[2}−		f(x)=−4
	2

Znalazłem takie x więc funkcja jest ciągła dla każdego x∊R Czy może tak byc?

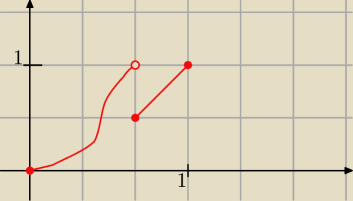
wredulus_pospolitus: absolutnie nie może tak być. 1. Czemu akurat taki przedział ? 2. Niech funkcja wygląda tak jak na wykresie −−− według Twego "mówimy krótko" ta funkcja jest ciągła na przedziale [0,1]

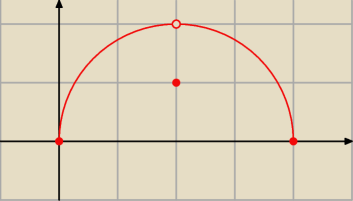
wredulus_pospolitus: Albo taka funkcja −−− ona także jest 'ciągła' wedle tejże 'zasady'. I w sumie każda funkcja niemonotoniczna, dla której znajdziemy takie a,b że f(a) = f(b) Kolejna sprawdza ... niech będzie, że jakaś funkcja jest ciągła w przedziale domkniętym [0,1] ... co to ma do ciągłości w zbiorze liczb rzeczywistych?

chichi: suma funkcji ciaglych jest funkcja ciagla. ciaglosc wielomianowej potraficie udowodnic?

#k: Podobny przykład miałem w swojej ksiązce . Jak wróce do domu to zobaczę jeszcze do innej Czyli to nie jest to twierdzenie z którego należy skorzystać

wredulus_pospolitus: Ten fakt służy nam do np. sprawdzenia czy ciągła funkcja f(x) przyjmuje wartość (np.) 7 w zadanym przedziale. Natomiast spełnienie danego faktu (a nie udowodniłeś że f(x) go spełnia) nie mówi nam o tym, że ta funkcja jest ciągła ... co zaprezentowałem na podstawie tych dwóch funkcji powyżej.

#k: Najpierw mam podaną taką definicję Mówimy że funkcja y=f(x) jest ciągła w punkcie x₀ jeżeli w punkcie tym nieskończenie małemu przyrostowi argumentu Δx odpowiada nieskończenie mały przyrost funkcji Δy a więc jesli lim Δy=lim [f(x₀+Δx)−f(x₀)]=0 Δx−−>0 Δx−−>0 G.I. Zaporożęc w swojej książce Metody rozwiązywania zadań z analizy matematycznej na stronie 62 pokazuje jak wykazać ze funkcja y=2x²−1 i funkcja v= cosec x sa ciągłe we wszystkich punktach swojego obszaru określoności My mamy funkcje y=x³+2x²−5 Dziedzinę mamy już określoną x∊ℛ czyli cała oś liczbowa i wychodząc z definicji ciągłości badamy czy funkcja jest w tym obszarze ciągła Weżmy więc dowolny przyrost (Δx) argumentu (x) i podstawiamy do danego wyrażenia funkcji zamiast (x) wartośc (x+Δx) wyznaczamy odpowiednią wartośc funkcji y+Δy=(x+Δx)³+2(x+Δx)²−5 Odejmujemy od tej wartości jej pierwotną wartośc znajdujemy przyrost funkcji (Δy) Δy=(x+Δx)³+2(x+Δx)²−5−(x³+2x²−5)= (Δx)³x³+3(Δx)²x³+2(Δx)²x²+3(Δx)x³+4(Δx)x² Niech teraz (Δx)→0 wtedy dla każdej wartości x mamy lim Δy=0 Δx→0 Zatem zgodnie z definicją ciągłości funkcji funkcja y=x³+2x²−5 jest ciągła dla dowolnej wartości x a więc w całym obszarze określoności