tym razem geometria Kinia: Podstawą Ostroslupa jest trójkąt prostokątny o kącie ostrym miary α i przeciwprostokatnej długości c. Wszystkie ściany boczne ostroslupa nachylone są do plaszcyzny podstaey jego podstawy pod tym samym kątem o mierze β. Oblicz pole powierzchni ostrosłupa. Wyznaczylam sb długość przyprostokatnych z podstawy i wysokosci ostroslupa. Teraz będę po kolei wyznaczać wsokosci ścian bocznych, ale to strasznie dużo pracy czy jest jakiś prostszy sposób Ratujcie !

Kinia: Możecie mi podpowiedzieć czy ściany boczne będą trojkatami rownoramiennymi?

Kinia: Hm?

Kinia: Podpowiedzcie mi proszę, jestem uparta no, bo wychodzi mi inaczej niż w odp i nwm gdzie mam błąd.

Bogdan: Ściany boczne nie muszą być trójkątami równoramiennymi, ale wysokości ścian bocznych poprowadzone od wierzchołka ostrosłupa maja równe długości. Ustal punkt w podstawie ostrosłupa, który jest spodkiem jego wysokości.

dero2005: Spodek wysokości będzie środkiem okręgu wpisanego w podstawę. Oblicz promień tego okręgu r. Stosunek promienia r do wysokości ściany bocznej jest równy cosβ. Z tego obliczysz wysokości ścian bocznych, które będą takie same dla wszystkich ścian. Mając boki podstawy i wysokość ściany bocznej obliczysz pole boczne. Do tego dodasz pole podstawy.

Kinia: No to co ja robię źle ? zrobilam jak Dero i właśnie mam zły wynik, inny niż w odpowiedziach

Kinia: Po kolei: długości boków podstawy: c, c sinα, c cosα

Kinia:

	c
Wysokość ściany bocznej:
	6cosβ

dero2005: jaki jest wynik w odpowiedzi?

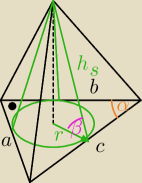
dero2005: a = c*sinα b = c*cosα

a*b		r(a+b+c)
	=
2		2

	csinαcosα
r =
	1 + sinα + cosα

	csinαcosα
hs =
	cosβ(1+sinα+cosα)

	a*b		c2
Pp =		=		sinαcosα
	2		2

	a*hs		b*hs		c*hs
Pb =		+		+
	2		2		2

itd

Kinia: Ale skoro c jest przeciwprostokatna to R=1/2c ja szłam z okręgu opisanego

dero2005: okrąg opisany stosuje się wtedy. gdy wszystkie krawędzie boczne są równe. wtedy spodek wysokosci wypada w środku okręgu opianego okręg wpisany − gdy ściany boczne są nachylone pod jednakowym kątem

Kinia: i stąd mój bląd − dzięki wielkie zawsze mam problem z tym spodkiem wysokości w ostrosłupach, no bo tak "normalnie" to co go wyznacza? Jest to punkt przecięcia środkowych ?