Pozdrawiam
Majkinek: Zbadaj liczbę pierwiastków równania w zależności od wartości parametru m.
a) |x2−2x−3|=m
proszę o pomoc
6 gru 20:06
Kacper:
Graficznie

6 gru 20:07
Majkinek: A trzeba dać założenie m>=0?
6 gru 20:09
Kacper:
To otrzymamy z rysunku

6 gru 20:09
Majkinek: A jeśli mielibyśmy liniową to wtedy też graficznie?

6 gru 20:10
Kacper:
Można

6 gru 20:11
Majkinek: Dziękuję bardzo

6 gru 20:11
Majkinek: A jak jak mam np przedzialy to mogę napisać m=i tutaj funkcje czy musze dawac np f(x)?
6 gru 20:23
Kacper:
Opisz dokładniej pytanie

6 gru 20:33
Majkinek: np rozpisuje wartość bezwzględną w przedziałach np x>=0 i x<0.. i w każdym wychodzi mi
odpowiednia funkcja dla przedziału...Czy mogę np... m=x2−2x+2...i potem na wykresie zaznaczyć
osie jako x i m?
6 gru 20:38
Tadeusz:
... ciężki "przypadek" −

6 gru 20:40
Kacper:
Osie masz x i y

|x|=m
Rysujemy dwa wykresy
y=|x| (wiadomo jak wygląda)
i
y=m (proste równoległe do osi x)
Na tej podstawie badasz liczbę rozwiązań równania.
Analogicznie twoje zadanie.
6 gru 20:41
Majkinek: Rozumiem

6 gru 20:42
Mila:
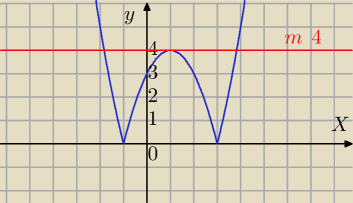
Narysuję, to co poradził Ci
Kacper
|x
2−2x−3|=m
f(x)=|x
2−2x−3|
x
w=1
|y
w|=4
Teraz odpowiedz na pytanie.
6 gru 23:46







 |x|=m
Rysujemy dwa wykresy
y=|x| (wiadomo jak wygląda)
i
y=m (proste równoległe do osi x)
Na tej podstawie badasz liczbę rozwiązań równania.
Analogicznie twoje zadanie.
|x|=m
Rysujemy dwa wykresy
y=|x| (wiadomo jak wygląda)
i
y=m (proste równoległe do osi x)
Na tej podstawie badasz liczbę rozwiązań równania.
Analogicznie twoje zadanie.

 Narysuję, to co poradził Ci Kacper
|x2−2x−3|=m
f(x)=|x2−2x−3|
xw=1
|yw|=4
Teraz odpowiedz na pytanie.
Narysuję, to co poradził Ci Kacper
|x2−2x−3|=m
f(x)=|x2−2x−3|
xw=1
|yw|=4
Teraz odpowiedz na pytanie.