Kolokwium z matematyka pomocy 5 zadan! Kuba: 1) sinx+√3cosx=1 2) 7^1−x+3*7^x+2>28

	1		1
3) 1−		=
	log2x		1−log2x

4) √x+1+1>x 5) Ix+2I<¹₂x+1 pomocy w tych 5 zadankach! chcialbym zobaczyc caly tok myslenia i dokladne rozwiazania,pozdrawiam serdecznie!

Basia: ad.1 dokładamy równanie sin²x+cos²x=1 prawdziwe dla każdego x∊R i rozwiązujemy układ równań sinx = 1−√3cosx (1−√3cosx)² + cos²x = 1 1 − 2√3cosx + 3cos²x + cos²x = 1 4cos²x − 2√3cosx =0 cosx(4cosx−2√3)=0 cosx = 0 lub 4cosx−2√3=0 cosx=0

	π
x0=
	2

	π
x =		+2kπ
	2

−−−−−−−−−−−−−−−−−−−−−−−−−−−− 4cosx − 2√3=0

	2√3
cosx =
	4

cosx = U{√3{2}

	π
x0 =
	6

	π
x =		+2kπ
	6

−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	π		π
Odp. x =		+2kπ lub x =		+2kπ
	2		6

========================================== ad.2 7^1−x+3*7^x+2 > 28 7¹*7^−x+3*7^x*7² > 28

7
	+ 3*49*7x > 28 /*7x
7x

7 + 3*49*(7x)² > 28*7^x /:7 1 + 3*7*(7^x)² > 4*7^x 21*(7^x)² − 4*7^x + 1 > 0 t = 7^x t>0 21t² − 4t + 1 > 0 Δ=16−4*21*1 =16−48 = −32 < 0 stąd: dla każdego t nierówność jest prawdziwa ⇒ nierówność (2) jest prawdziwa dla każdego x∊R ======================================== ad.3 założenia: x>0 log₂x≠0 ⇔ log₂x≠log₂1 ⇔ x≠1 1−log₂x≠0 1≠log₂x log₂x≠log₂2 x≠2 x>0 ∧ x≠1 ∧ x≠2 −−−−−−−−−−−−−−−−−−−−−−−

	1		1
1−		=		/*log2x*(1−log2x)
	log2x		1−log2x

log₂x*(1−log₂x) − (1−log₂x) = log₂x log₂x − (log₂x)² − 1 + log₂x − log₂x = 0 −(log₂x)² + log₂x − 1 = 0 t = log₂x −t² + t − 1 = 0 Δ=1¹−4*(−1)*(−1) Δ=1−4 = −3 równanie nie ma rozwiązania ========================== ad.4 √x+1+1>x x+1≥0 x≥−1 −−−−−−−−−− √x+1>x−1 (√x+1)²>(x−1)² x+1 > x²−2x+1 x²−3x<0 x(x−3)<0 x∊(0;3) ======================= ad.5 |x+2|<¹₂x+1 1. x+2≥0 ⇔ x≥−2 |x+2| = x+2 x+2<¹₂x+1 ¹₂x < −1 /*2 x<−2 sprzeczne z założeniem czyli w tym przypadku nierówność nie ma rozwiązania 2. x+2<0 ⇔ x<−2 |x+2| = −(x+2) = −x−2 −x−2<¹₂x+1 −³₂x < 3 /:(−³₂ czyli *(−²₃) x > −2 sprzeczne z założeniem czyli w tym przypadku nierówność również nie ma rozwiązania odp. nierówność nie ma rozwiązania

Misiek: dzieki wielkie!

AS: sinx + √3*cosx = 1 Sposób 1. Podstawiam tgα = √3 → α = π/3 sinx +tgα*cosx = 1

	sinα
sinx +		*cosx = 1 |*cosα
	cosα

sinx*cosα + cosx*sinα = cosα sin(x + α) = cosα = 1/2 x1 + π/3 = π/6 + 2*k*π , k ∊ C x2 + π/3 = π − π/6 = 2*k*π x1 = − π/6 + 2*k*π x2 = π/2 + 2*k*π Sposób 2 Stosuję podstawienie

	2*t		1 − t2
sinx =		, cosx =		gdzie t = tg(x/2)
	1 − t2		1 + t2

2*t		1 − t2
	+ √3*		= 1 |*(1 + t2)
1 + t2		1 + t2

2*t + √3 − √3*t² = 1 + t² (1 + √3)*t² − 2*t + 1 − √3 = 0 Δ = (−2)² − 4*(1 + √3)*(1 − √3) = 4 − 4*(1 − 3) = 12 , √Δ = p[12] = 2*√3

	2 − 2*√3		1 − √3
t1 =		=
	2*(1 + √3)		1 + √3

tg(x1/2) = tg(−15^o) ⇒ x1/2 = −15^o + k*90^o ⇒ x1 = −30⁰ + 2*k*180^o , k ∊ C

	2 + 2*√3		1 + √3
t2 =		=		= 1
	2*(1 + √3)		1 + √3

tg(x2/2) = tg(45^o) ⇒ x2/2 = 45^o + k*180^o ⇒ x2 = 90^o + 2*k*180^o , k ∊ C

AS: Korekta: x2 + π/3 = π − π/6 + 2*k*π

	2*t
sinx =
	1 + t2

Misiek: as czyli Basia dobrze wyliczyla czy nie ?

AS: Przykre,ale Basia popełniła błąd, π/6 nie spełnia tego równania. Przeoczyła fakt,że jest to pierwiastek obcy.

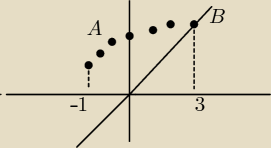
AS: Ciekawy przypadek w zad. 4. Odpowiedzią jest (−1,3) ale nie znalazłem uzasadnienia rachunkowego. A: wykres funkcji y = √x + 1 + 1 B: wykres funkcji y = x W obszarze (−1,3) wartości funkcji A są większe od wartości funkcji B

BiebrzaFun : może tak? √x+1+1>x zał x+1≥0 x≥−1 √x+1>x+1−1−1 √x+1=t −t²+t+2>0 t₁=2 t₂=−1 −1<t<2 −1<√x+1<2⇒−1<√x+1 x∊R i x≥−1⇒x≥−1 √x+1<2 ⇒x<3 odp x∊<−1,3)

BiebrzaFun : gdzie jest błąd w rozw. Basi? x=−1 spełnia nie−ść

KoK: Basia zapomniała, źe x jest również x≥−1 ,co daje wraz z x∊(0;3) ⇒ x∊<−1,3)

AROB: Taki błąd się zdarza, gdy podnosi się nierówność obustronnie do kwadratu, a nie ma pewności co do znaku obu stron. Tu prawa strona , czyli (x−1) dla x= −1 właśnie jest ujemna, a dla innych x jest dodatnia. A po podniesieniu do kwadratu ginie to rozwiązanie. Po prostu, trzeba bardzo ostrożnie używać podnoszenia do kwadratu nierówności. Metoda BiebrzaFun jest bezpieczniejsza i dała poprawny wynik.

AROB: Postanowiłam dodać uzupełnienie, gdyż wiem, ile kłopotu sprawia rozwiązywanie nierówności niewymiernych. Otóż rozwiązując nierówność niewymierną można podnosić do kwadratu obie jej strony tylko wtedy, gdy mają one ten sam znak. Kierunek nierówności określa następująca zasada: gdy a < b i a,b są dodatnie, to a² < b², gdy a < b i a,b są ujemne , to a² > b², gdy a < b i a,b są różnych znaków , to nie ma stałego związku między liczbami a,b oraz ich kwadratami. Należy wtedy rozpatrywać 2 przypadki. Pokażę użycie tej zasady do zadania rozwiązanego już powyżej. √x + 1 + 1 > x Założenie: x + 1 ≥ 0 ⇒ x ≥ −1 √x + 1 > x − 1 Lewa strona nierówności jest nieujemna na mocy definicji pierwiastka kwadratowego dla wszystkich x należących do dziedziny, a strona prawa przyjmuje różne znaki, zatem trzeba rozważyć 2 przypadki. 1⁰. Gdy x − 1 ≥ 0 , czyli x ≥ 1 mamy: (√x + 1)² > (x − 1)² x + 1 > x² − 2x + 1 x² − 3x < 0 x(x − 3) < 0 ⇒ x ∊ (0, 3) Uwzględniając założenie przyp. 1⁰ oraz dziedzinę otrzymamy: (0, 3) ∧ (x ≤ 1) ∧ (x ≥ −1 ) ⇒ x ∊ < 1, 3) 2⁰. Gdy x − 1 < 0 , czyli x < 1, nierówność zachodzi w sposób oczywisty, ponieważ prawa strona nierówności jest wtedy ujemna , a lewa dodatnia. Zatem nierówność jest spełniona dla wszystkich x należących do dziedziny, czyli dla x ≥ −1. Składając oba założenia: (x < 1) ∧ (x ≥ −1) otrzymamy: x ∊ <−1,1). Łącząc oba przypadki jako sumę otrzymanych przedziałów otrzymujemy ostateczne rozwiązanie nierówności: <1, 3) ∪ < −1, 1) = < −1, 3) Odp. x ∊ < −1, 3)

AROB:

Nestor: Superr objaśnione

AS: Uzupełniam wywody swoimi spostrzeżeniami Gdy a i b są różnych znaków i a < b oraz |a| < |b| to a² < b² np. −4 < 5 , |−4| < |5| , (−4)² < 5² , 16 < 25 a < b oraz |a| > |b| to a² > b² np −8 < 6 , |−8| > |6| , (−8)² > 6² , 64 > 36

AROB:

AROB: Żegnam wszystkich, a szczególnie ABBĘ. Dobrej nocy!

Bogdan: Ja również życzę dobrej nocy

Basia: ad.1 Błąd jest gdzie indziej do momentu

	√3
cosx=		jest dobrze
	2

teraz:

	√3		3		1
sinx = 1−√3*		= 1−		= −
	2		2		2

	1		√3
sinx=−		i cosx =		⇒ czwarta ćwiartka czyli
	2		2

	π		11π
x0 = 2π−		=
	6		6

	11π
x =		+2kπ
	6