Nierówność Nieróność:

m2
	>1
4−m

Proszę o pomoc. Próbowałem zamienićna iloczyn ale nie wiem co dalej ( przez co podzielić i jak znaleźć rozwiązania ) .

J: założenie m ≠ 4

	m2
⇔		− 1 > 0 .. teraz wspólny mianownik ...
	4 −m

Nieróność: Dobra, całkowicie zapomniałem o wspólnym mianowniku dziękuję

Nieróność: A jak mianownik jest podniesiony do kwadratu ? Postępowanie to samo? Jeśli tak, to wyszło mi : 8m³−80m²+256m−256>0 I dalej trzeba dzielników szukać?

razor: zapisz przykład

Nieróność:

m2
	>1
(4−m)2

Nieróność: Pomoże ktoś?

pigor: ... , widzę to np. tak:

m2
	>1 /*(4−m)2 i (*) m≠4 ⇒ m2}(4−m) >(4−m)2 ⇒
4−m

⇒ m²(4−m) − (4−m)² >0 ⇔ (4−m)(m²−4+m) >0 ⇔ ⇔ −(m−4)(m²+m−4) >0 ⇔ (m−4)(m²+m−4)< 0 i tu brzydka "delta" (wyróżnik) to dalej już może sam(a), bo ja znikam z forum....

Gamers: a po co podniosłes do kwadratu mianownik

Nieróność: (m−4)(m2+m−4)< 0 Jeżeli (m−4) < 0 lub (m2+m−4)< 0 Później z tego zrobić sumę? I będzie m?

Nieróność: Nie wiem, nie wychdzi mi to

Nieróność: Jak będziecie mieli czas, to proszę, spróbujcie pomóc Pozdrawiam

jakubs: Nie no jak masz lub, to nie sumuj

Nieróność: Dalej nie wychodzi

Piotrek: weźcie, to nie tak

Nieróność: a jak?: )

Piotrek:

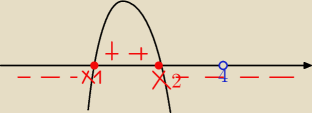
m2
	>1 ⇔ m2>4−m ⇔ −m2−m+4<0
4−m

Δ=1−4*(−1)*4=17

	1+√17		1−√17
x1=		x2=
	−2		−2

wspolczynnik a jest ujemny wiec ramiona w dół a m∊(−∞,x₁)∪(x₂,4)∪(4,+∞)

Piotrek: U góry to jakiś masochizm

Piotrek: Niewiem czy to dobrze u góry bo nawet niechce mi sie sprawdzac

Piotrek: Oczywiście Dziedzina to R−{4} i trzeba wziąśc potem czesc wspolna z nierownościa

Piotrek: Rozumiesz to?

Nieróność: To można obie strony przemnożyć przez (4−m) ? Bo my mówimy tu o kwadracie

m2
	>1 To da dalsza nierówność
(4−m)2

Piotrek: o kwadracie?, w pierwszym poscie nie napisaes kwadratu w mianowniku

Piotrek: W sumie to to co napisalem to pierwszy przypadek

Nieróność: Wiem, ale pierwszy post już ktoś mi opisał wcześniej i nie wiem czy dobrze z tym wspólnym mianownikiem. W kolejnym poście zapytałem, jak by to wyglądało dla kwadratu w mianowniku i podałem powyższy wzór

Piotrek: pomnoz przez ten minownik obustronnie bo to dodatnie tak czy siak

Nieróność: Ok , wyszło dzięki