prawdopodobieństwo madzik: Z urny zawierającej 6 kul białych, 3 czarne i 5 niebieskich losujemy 1 kulę. Następnie dokładamy do urny 2 kule w kolorze wylosowanej kuli i ponownie losujemy 1 kulę. Oblicz prawdopodobieństwo, że kula wylosowana za drugim razem będzie niebieska. Jak to najsensowniej rozwiązać i rozrysować na drzewku?

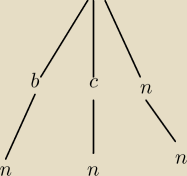
irena_1: Ponieważ interesuje nas tylko wylosowanie kuli niebieskiej, więc można narysować skrócone drzewko. Górne gałęzie to pierwsze losowanie :

	6
− n z prawdopodobieństwem
	14

	3
− c z prawdopodobieństwem
	14

	5
− n z prawdopodobieństwem
	14

Dolne gałęzie to losowanie kuli niebieskiej za drugim razem. Mamy teraz 16 kul. W dwóch pierwszych przypadkach wśród nich jest 5 kul niebieskich, więc prawdopodobieństwo

	5
wylosowania kuli niebieskiej to		.
	16

	7
W trzecim − mamy wśród 16 kul 7 niebieskich, więc tu prawdopodobieństwo jest równe
	16

	6		5		3		5		5		7		30+15+35
P(A)=		*		+		*		+		*		=		=
	14		16		14		16		14		16		224

	80		5
=		=
	224		14