Zastosowanie analizy matematycznej w rozwiązywaniu zadań z geometri analitycznej CudMalina: Witam. Mam problem z takim oto zadankiem. Nie bardzo wiem jak wyznaczyć funkcję opisującą zależność pola od x. Ma ktoś jakiś pomysł? Będę bardzo wdzięczna. (: Wśród prostokątów, których dwa wierzchołki należą do paraboli o równaniu y=(x+3)², zaś dwa pozostałe na prostej k: y=4, znajduje się taki, którego pole jest największe. Oblicz współrzędne wierzchołków tego prostokąta i jego pole.

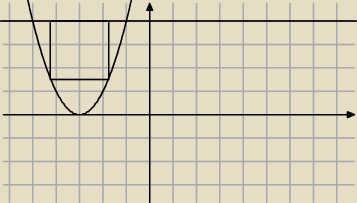
Kacper: Masz rysunka

CudMalina: Rysunek to ja zrobiłam na początku. : p

tio: czyżby ekstrema warunkowe funkcji 2 zmiennych ?

PW: No, czyli w tym wypadku trzeba ułożyć wzór opisujący zależność pola nie od x, ale od u, gdzie y = u jest równaniem tej prostej leżącej niżej − ona wyznaczy (w miejscach wspólnych z parabolą) dwa wierzchołki prostokąta, a więc jego podstawę. Wysokość prostokąta to 4 − u.

CudMalina: Okej, to ma sens. Jak?

PW: 1° Punkty wspólne paraboli y = (x+3)³ i prostej y = u − dostaniemy dwa punkty o współrzędnych zależnych od u. 2° Odległość tych punktów (zależna oczywiście od u) to podstawa prostokąta.

CudMalina: No dobrze, czyli jakie powinny być współrzędne tych punktów?

PW: A ... to chciałaś gotowca, a nie wskazówki? Rozwiąż układ równań

	⎧	y=(x+3)2
	⎨
	⎩	y = u

z parametrem u, czyli po prostu podstaw u zamiast y w pierwszym równaniu i wylicz iksy.

CudMalina: Nie chodzi o gotowca, po prostu nie bardzo wiem co z tym zrobić. Policzyłam tak wcześniej i wychodzi mi, że x=√u−3, a to tylko jeden x. Chodzi o to, że x+3 powinno być wartością bezwzględną? I wtedy dojdzie do tego x=−√u−3

PW: Jjjjaaasne. No to teraz podstawa prostokąta: odległość między punktami (−√u−3, u) i (√u−3, u)

CudMalina: Teraz wreszcie coś udało się policzyć. Dzięki wielkie. (: