Granice Funkcji ;)
Hajtowy: Granice funkcji − zadania studenckie xd

Będzie miał ktoś jutro chęci i czas by poświęcić go na przerobienie ze mną kilkunastu zadań z
granicy funkcji do kolokwium?


4 gru 20:13
olala:

4 gru 20:14
Kacper: 
4 gru 20:18
Mila:
Pisz zadania.
4 gru 20:22
Hajtowy: Nie miałem tego w liceum tylko przez 1h na ćwiczeniach bez wykładu z tego tematu także mogą być
lekkie problemy dlatego prosiłbym o wyjaśnienia i wyrozumiałość


Obliczyć granicę w punkcie:
"Uczono" mnie,że podstawiamy za 'x' to do czego dąży 'x' czyli w tym przypadku 1.
| | 1 | | 1 | | 5 | |
limx→1 (x3+2x− |
| ) = 1+2− |
| = |
| |
| | 2 | | 2 | | 2 | |
I to tyle czy coś więcej?

4 gru 20:29
Kacper:
Wszystkie wielomiany, to funkcje ciągłe, zatem granica w punkcie, to po prostu wartość dla
danego argumentu

4 gru 20:30
Hajtowy: | | 7 | |
No ale w odpowiedzi mam: − |
| |
| | 2 | |
4 gru 20:32
Kacper:
To zapewne granica była w −1, a nie 1

4 gru 20:34
Hajtowy: A no −1

4 gru 20:34
Hajtowy:
| | (x+2)2 | | 0 | |
b) limx→−2 |
| = |
| |
| | x2−4 | | 0 | |
4 gru 20:36
olala:
A teraz

| (x+2)(x+2) | |
| =............... |
| (x+2)(x−2) | |
4 gru 20:37
Hajtowy:
| | (x+2)2 | | x+2 | | 0 | |
= limx→−2 |
| =limx→−2 |
| = |
| = 0 ? |
| | (x−2)(x+2) | | x−2 | | −4 | |
4 gru 20:37
Kacper:

4 gru 20:39
olala:
ok
4 gru 20:39
Hajtowy:
| | x2+5x−6 | | 0 | |
c) limx→1 |
| =[ |
| ] = |
| | x2+4x−5 | | 0 | |
| | (x−1)(x+6) | | x+6 | | 7 | |
= limx→1 |
| = |
| = |
| ?  |
| | (x−1)(x+5) | | x+6 | | 6 | |
4 gru 20:41
olala:
ok

( tylko popraw chochlika)
4 gru 20:42
Hajtowy: x+5 w mianowniku

4 gru 20:43
Hajtowy:
| | 2x2−10x+12 | | 0 | |
d) limx→3 |
| = [ |
| ] = |
| | x3−2x2−3x | | 0 | |
| | 2(x−3)(x−2) | | 2(x−2) | | 2 | | 1 | |
= limx→3 |
| = |
| = |
| = |
| |
| | x(x−3)(x+1) | | x(x+1) | | 12 | | 6 | |
Dobrze?

4 gru 20:54
Kacper: 
4 gru 20:55
olala:
Zdolny studencik 
4 gru 20:59
Hajtowy: zaczynają się schody

| | x−3 | | 0 | |
h) limx→3 |
| = [ |
| ] = |
| | √x−√3 | | 0 | |
| | x−3 | | √x+√3 | | problem | |
limx→3 |
| * |
| = |
| = KŁOPOT  |
| | √x−√3 | | √x+√3 | | x−3 | |
a ten problem =
√x2+
√3x−3
√x−3
√3 ?

Czy coś innego ?

Co by nie było dalej i tak jest KŁOPOT

4 gru 21:00
Kacper:
| | a2−b2 | |
Skorzystaj z wzoru a+b= |
| |
| | a−b | |
4 gru 21:02
olala:
x−3=(√x−√3)(√x+√3)
4 gru 21:04
Hajtowy: olala no wiem, tylko że mi coś wyjść nie chce

| | √x2+√3x−3√x−3√3 | |
Bo mam |
| =... a gdy teraz podstawię za 'x' trójkę to coś mi wynik |
| | x−3 | |
się nie zgadza

4 gru 21:07
olala:
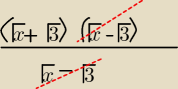
4 gru 21:11
Hajtowy: Haha

nie zauważyłem tego

4 gru 21:11
olala:

4 gru 21:12
Kacper:

4 gru 21:13
olala:

4 gru 21:14
Hajtowy:
Wtedy mi zostanie?
| √x+√3*√x+√3 | |
| = √3+ √3=2 √3 ?  |
| √x+√3 | |
4 gru 21:15
olala:
Znowu masz chochlika

4 gru 21:16
Hajtowy: gdzie?

wynik mam dobry xd
4 gru 21:17
olala:
A no ano , jest ok

4 gru 21:18
Hajtowy:
| | x+√x | | 0 | |
i) limx→0+ |
| = [ |
| ] |
| | x−√x | | 0 | |
To jest granica jednostronna w punkcie?

Bo nie wiem co dalej

4 gru 21:19
Marcin: | x+√x | | | |
| ⇔ |
| , może to jakoś pomoże  |
| x−√x | | | |
4 gru 21:25
Hajtowy: Przypomina mi się liczba 'e'

zaraz pokombinuje

4 gru 21:27
Mila:
| (x+√x)*(x+√x) | | x2+2x√x+x | |
| = |
| = dokończ |
| x2−x | | x*(x−1) | |
4 gru 21:33
Hajtowy: ooo to tak też można?


4 gru 21:34
Lukas:
olala gdzie Eta ?

4 gru 21:36
olala:

a już miałam to samo pisać (
Mila 
4 gru 21:36
olala:
Olalalala

4 gru 21:37
Hajtowy:
Mila odpowiadam

| | x(x+2√x+1 | | 2√0+1 | | 1 | |
= |
| = |
| = |
| =−1 ?  |
| | x(x−1) | | x−1 | | −1 | |
4 gru 21:39
Hajtowy:
| | √x2+1−1 | | 0 | |
j) limx→0 |
| = [ |
| ] |
| | √x2+4−2 | | 0 | |
Mila jakiś sposób podobny i krótki na ten wzór?

Bo tutaj chyba trzeba do 3 potęgi zastosować

4 gru 21:46
olala:
| (√2+1−1)(√x2+1+1) | | (√x2+4+2) | |
| * |
| =.... |
| (√x2+4−2)(√x2+4+2) | | (√x2+1+1) | |
4 gru 21:51
Mila:
Nie ma specjalnych dróg dla
Hajtowych, trzeba się pomęczyć .
| √x2+1−1 | | √x2+1+1 | | √x2+4+2 | |
| * |
| * |
| |
| √x2+4−2 | | √x2+1+1 | | √x2+4+2 | |
4 gru 21:54
Hajtowy:
| | √x2+4+2 | |
= 1* |
| = 2 ?  |
| | √x2+1+1 | |
4 gru 21:57
Saizou :
tak, jeśli się nie pomyliłem licząc

4 gru 21:58
4 gru 21:58
olala:
Ok ...... g=2
4 gru 22:00
Hajtowy:
| | √x−1−(x−1) | | 0 | |
k) limx→2 |
| = [ |
| ] |
| | x−2 | | 0 | |
Pytanie jak to ruszyć, bo nie widzę na razie tutaj rozwiązania

ten pierwiastek mi
przeszkadza xd

4 gru 22:01
Saizou :
korzystasz ze wzorku (a−b)(a+b)=a
2−b
2
| | (√x2+1−1)(√x2+1+1) | | x2 | |
licznik: √x2+1−1= |
| = |
| |
| | √x2+1+1 | | √x2+1+1 | |
analogicznie mianownik
4 gru 22:04
Hajtowy:
hmm...
Saizou nie zbyt ogarniam coś Ty zrobił

4 gru 22:06
olala:
Pomnóż licznik i mianownik przez sprzężenie licznika, czyli przez (√x−1+(x−1)]
zobaczysz ,że w liczniku otrzymasz czynnik ( x−2)(......)
4 gru 22:07
4 gru 22:11
Hajtowy: | −(x−2)(x−1) | | 1 | |
| =− |
| |
| √x−1(x−2)+x−1 | | 2 | |
4 gru 22:14
olala:


4 gru 22:15
Saizou :
olala co tam słychać? nie brakuje jabłuszek
Eta ?
ale nie róbmy
Hajtowemu spamu tu

4 gru 22:17
Hajtowy: 11 przykładów z tego zadania + inne JUTRO

Niestety jutrzejszy wf na 7:00 zmusza mnie do GŁĘBOKIEGO


aby się wyspać

Dziękuję wszystkim za pomoc dzisiejszą


Jutro się odezwę!

4 gru 22:18
Saizou :
To miłego i śpij dobrze, przed w−f trzeba być wypoczętym, powiedział student, który zajęcia z
wychowania fizycznego ma w drugim semestrze

4 gru 22:21
Hajtowy: Witam witam

Nowy dzień, nowe wyzwania

| | √1−2x−x2−(1+x) | | 0 | |
l) limx→0 |
| = [ |
| ] = |
| | 2x | | 0 | |
| | √1−2x−x2−(1+x) | | √1−2x−x2+(1+x) | |
limx→0 |
| * |
| = |
| | 2x | | √1−2x−x2+(1+x) | |
No i tutaj jest mały problem... czy to ma wyglądać tak, że:
| | a2−b2 | |
= |
| |
| | 2x(√1−2x−x2+(1+x)) | |
Z czym, że
a=
√1−2x−x2 ; a
2 = 1−2x−x
2
b=−1−x ; b
2 = 1−x
2 ?
5 gru 10:12
Gray: b2=(1+x)2; reszta OK
5 gru 10:41
Hajtowy: 1−2x−x
2 − (x
2+2x+1)
| −2x2−4x−2 | | −2 | |
| = |
| =−1? |
| 2x(√1−2x−x2+(1+x)) | | 2 | |
5 gru 11:11
Saizou : coś nie tak z tym mianownikiem jest

policz jeszcze raz 1−1

5 gru 11:17
Hajtowy: | | −2 | |
Mówisz, że będzie |
| = −2 ?  |
| | 1 | |
5 gru 11:28
Hajtowy: Nie no kurde

Nawet 0 wychodzi z tego xd

5 gru 11:31
Saizou :
policz a nie zgaduj

| √1−2x−x2−(1+x) | | √1−2x−x2+(1+x) | |
| • |
| = |
| 2x | | √1−2x−x2+(1+x) | |
| √1−2x−x22−(1+x)2 | | 1−2x−x2−(1+2x+x2) | |
| = |
| = |
| 2x[√1−2x−x2+(1+x)] | | 2x[√1−2x−x2+(x+1)] | |
| 1−2x−x2−1−2x−x2 | | −2x2−4x | |
| = |
| = |
| 2x[√1−2x−x2+(x+1)] | | 2x[√1−2x−x2+(x+1)] | |
| −2x(x+2) | | −(x+2) | | −2 | |
| = |
| → |
| =−1 przy x→0 |
| 2x[√1−2x−x2+(x+1)] | | √1−2x−x2+(x+1) | | 2 | |
5 gru 11:34
Hajtowy: A no fakt... źle sobie policzyłem

<zalmka> takie głupie błędy...
No ale lecim dalej!

No to sprzężeniem?

5 gru 11:45
Hajtowy: lim
x→−1 ma być !

5 gru 11:50
Saizou : pomyśl trochę

5 gru 11:51
Saizou :
no tak mnożenie przez sprzężenie, ale czego, licznika czy mianownika?
5 gru 11:53
Hajtowy: Wyszło mi z tego 0 ...

| | x+1 | | √x+5+(x+3) | |
limx→−1 |
| * |
| = |
| | √x+5−(x+3) | | √x+5+(x+3) | |
| | x2+2x+1 − (x+5+x+3) | |
= limx→−1 |
| ...  |
| | −x2−5x−4 | |
5 gru 11:56
Hajtowy: coś mi się to nie podoba za bardzo

5 gru 12:02
Saizou :
zauważ że −1 zeruje mianownik, zatem −1 jest pierwiastkiem wielomianu −x2−5x−4
a no i popraw licznik
5 gru 12:02
Hajtowy:
Ale co w tym liczniku jest znów nie tak?

5 gru 12:07
Saizou :
a to co za herezja

(x+1)(
√x+5+(x+3)) ≠ x
2+2x+1−(x+5+x+3)
5 gru 12:09
Hajtowy:
| | x2+√x+5x+4x+√x+5+3 | | 8 | |
... = |
| = − |
| ? |
| | −[(x+4)(x−1)] | | 6 | |
5 gru 12:14
Saizou :
ale po co to wymnażasz

, skoro (x+1) się skróci,
−x
2−5x−4≠ −((x+4)(x−1))
tylko
−(x
2+5+4)=−(x+1)(x+4)
5 gru 12:26
Saizou : ja mykam na razie, będę tak za 30 min
5 gru 12:29
Hajtowy: Wyszło


5 gru 12:36
Hajtowy:
| | sin2x | |
n) limx→0 |
| = ...  |
| | 3x | |
5 gru 12:38
jakubs: zaraz pomoge

5 gru 12:42
Hajtowy: spoko

tak się zastanawiam co to wgl jest xd

Wiem, że gdy
Tak nam podano xd

5 gru 12:46
jakubs: | | sin2x * 2x | |
limx→0 |
| = |
| | 3x * 2x | |
| | sin2x | | 2x | |
limx→0 |
| * |
| =..?  |
| | 2x | | 3x | |
5 gru 12:47
Hajtowy: | | 2 | |
czyli po prostu wyjdzie z tego |
| czy mi się wydaje?  |
| | 3 | |
5 gru 12:47
jakubs: No i korzystasz z tego, bo analogicznie zachodzi coś takiego:
| | sin(nx) | |
limx→0 |
| =1 dla n∊ℕ |
| | nx | |
5 gru 12:48
jakubs: Tak

5 gru 12:49
Hajtowy:
| | sinx2 | | 1 | |
Mogę to zapisać jako: limx→0 |
| = |
| ? |
| | 3x2 | | 3 | |
5 gru 12:50
jakubs: tam jest (sinx)2, czy sin(x2) ?
5 gru 12:52
Hajtowy: sin
2x

5 gru 12:52
Hajtowy: tylko ja sobie później z tego zrobiłem sinx
2 
xD

5 gru 12:53
jakubs: Wynik OK

5 gru 13:08
Hajtowy:
Next

A z tym cudem co zrobimy ?

5 gru 13:17
jakubs: Trzeba coś zrobić z mianownikiem

| | sin2x4 | | sin33x | | 1 | | 27 | |
limx→0 |
| * |
| * |
| = |
| |
| | x216 | | 27*x3 | | 3227 | | 32 | |
5 gru 13:28
Hajtowy: Jaka magia


Ale wyszło pięknie

5 gru 13:33
jakubs: Trzeba troszkę kombinować, ale spoko jak przyjdą pochodne to będzie łatwiej, bo są schematyczne

5 gru 13:42
Hajtowy:
| | sin2x | | 0 | |
r) limx→0 |
| = [ |
| ] = lim x→0 ... ?  |
| | √x+9−3 | | 0 | |
Sprzężenie? ale ten sin2x to wredne mi przeszkadza

5 gru 14:30
jakubs: | | 2*sin2x(√x+9+3) | |
limx→0 |
| =12  |
| | 2x | |
5 gru 14:34
bezendu:

5 gru 14:36
Hajtowy: A mogę wiedzieć skąd w mianowniku wzięło się nagle 2x i 2 przed sin2x?

bo dla mnie to
ciężkie na poczatku

5 gru 14:37
bezendu:
x→0
sin2x
| sin2x | |
| *2x dopisuję żeby nie zmienić |
| 2x | |
5 gru 14:43
jakubs: Ze sprzężenia otrzymasz bez tych dwójek, ja rozszerzyłem licznik i mianownik o tę dwójkę aby
pozbyć się sinusa

5 gru 14:43
Hajtowy: dobry pomysł

Ty jednak
jakubs myślisz dobrze



No to lecim dalej!

Pomysłu żadnego nie mam... trygonometria się kłania ale leży

5 gru 14:46
bezendu:
Poczekaj na pochodne albo na całki wtedy nauczysz się trygonometrii

5 gru 14:50
Hajtowy: pochodne będa po kolosie w czwartek

5 gru 14:53
jakubs: Ja tutaj nie mam pomysłu, robiłbym tutaj z de l'Hospitala.
5 gru 15:01
Hajtowy: Nie znam tego "KOLEGI"


Robie dalej inne, jak bd miał problem to napiszę

5 gru 15:03
Hajtowy:
Oblicz granice funkcji w nieskończoności...

Zaplątałem się w przykładzie N

5 gru 15:17
Hajtowy: Podzielić przez x
2 ?

5 gru 15:19
jakubs: Wyciągnij z pierwiastka x
2 i zobacz, czy na pewno podzielić przez x
2 
5 gru 15:22
razor: pamiętaj że √x2 = |x| a nie x
5 gru 15:23
Hajtowy: Chyba mam jakieś chwilowe zaćmienie

13 przykładów z tego typu zadań i to mnie zatrzymało...
no kurde no nie wiem!

5 gru 15:25
5 gru 15:28
Mila:
o) z 12:50 tak zapisz:
| | sin2x | | sinx | | 1 | | 1 | | 1 | |
lim x→0 |
| =lim x→0( |
| )2* |
| =1* |
| = |
| |
| | 3x2 | | x | | 3 | | 3 | | 3 | |
5 gru 15:30
Hajtowy: czemu
√x2 =−x

?
5 gru 15:31
5 gru 15:32
razor: √x2 = |x| = −x dla x < 0
5 gru 15:32
Mila:
| | tg(2x)−sin(2x) | |
s) lim x→0 |
| |
| | x3 | |
Taka granica?
5 gru 15:34
Hajtowy: Mila tak

5 gru 15:34
Hajtowy: | | 1 | |
razor i teraz mogę podzielić przez 'x' i wyjdzie mi |
| =−1*(−1) = 1 ? |
| | −1 | |
5 gru 15:36
5 gru 15:38
Hajtowy:
zad 3
| | √x+4−√x−4 | | √x+4+√x−4 | |
o) limx→∞ (√x+4−√x−4) = limx→∞ |
| * |
| = |
| | 1 | | √x+4+√x−4 | |
| | x+4−x+4 | |
= limx→∞ |
| = ? |
| | √x+4+√x−4 | |
Dobrze wgl myślę?

5 gru 15:40
Hajtowy: razor no ale granica jest −
∞ 
5 gru 15:40
razor: iksy się skracają i co zostaje?
5 gru 15:42
Hajtowy:
| 8 | |
| no i co z tymi pierwiastkami znowu zrobić? znów sprzężenie?  |
| √x+4+√x−4 | |
5 gru 15:44
5 gru 15:44
razor: moje pytanie było do poprzedniego przykładu ale tu jest dobrze
5 gru 15:45
jakubs: Dokładnie tak jak w poście z 15:44

5 gru 15:45
razor: | | | sin2x(1−cos22x) | |
| | | cos2x(1+cos2x) | |
| | sin32x | | 1 | |
|
| = |
| * |
| = |
| | x3 | | x3 | | cos2x(1+cos2x) | |
| | sin2x | | 8 | | 8 | |
( |
| 3) |
| → [1* |
| ] = 4 |
| | 2x | | cos2x(1+cos2x) | | 1*(1+1) | |
5 gru 15:46
razor: zgadza się z odpowiedzią? bo nie chciało mi się sprawdzać

5 gru 15:47
Hajtowy:
| | 1+2/x | | 1 | |
A tam zostaje mi |
| = |
| = −1 |
| | −1 * √1+3/x | | −1 | |
No ale skoro granica dąży do −
∞ to znak na końcu się zmienia (tak nas uczono)

5 gru 15:47
Mila:
cd. (s)
| | | | 1−cos2x+sin2x | | 2sinx*cosx* |
| | | | cos(2x) | |
| |
=limx→0 |
| = |
| | x3 | |
| | 2sinx*2sin2x | | sinx | | 4 | |
=limx→0 |
| = limx→0( |
| )3* |
| =4 |
| | x3 cos(2x) | | x | | cos(2x) | |
5 gru 15:47
Hajtowy: @15:46 zgadza się


5 gru 15:48
razor: to masz rozwiązane na 2 sposoby

5 gru 15:48
Mila:
To ja uciekam stąd.
5 gru 15:50
Hajtowy: Dziękuję
Mila 

przykład Q

q) lim
x→∞ 3√x3+2x2−
3√x3−2
Wiem, że mogę to sprzężeniem zrobić, ale też jest wzór na a
3−b
3? Dobrze kojarzę?
5 gru 15:51
5 gru 15:52
Hajtowy: dokładnie to

dzięki

5 gru 15:56
jakubs: Ja na to nie wpadłem

5 gru 15:56
Hajtowy: Ale i tak chyba zrobie to sprzężeniem, bo te wzory do
3 mi nie idą ostatnio wgl xd
jakubs nie martw się

5 gru 15:58
razor: jak to sprzężeniem?
5 gru 15:59
Hajtowy: ale sprzężeniem nie idzie to pewno trzeba tym głupim wzorem co podałeś

5 gru 16:02
Hajtowy: dobra ciul z tym przykładem, za głupi

A tutaj...?

5 gru 16:08
jakubs: Wyciągnij x
2 z pierwiastka.
q) to tylko wzór skróconego mnożenia, nie poddawaj się

5 gru 16:09
Hajtowy:
O to chodziło
jakubs?

5 gru 16:11
Mila:
r)
| | √x2+15−6 | | √x2+15+6 | |
lim x→∞ |
| * |
| = |
| | x+3 | | √x2+15+6 | |
| | x2+15−36 | |
=lim x→∞ |
| =..... dokończ |
| | (x+3)*√x2+15+6) | |
5 gru 16:19
Hajtowy:
| | x2−21 | |
= |
| |
| | x√x2+15+ 3√x2+15+6x−18 | |
5 gru 16:23
jakubs: | | x√1+15/x−6 | | √1+15/x−6/x | |
limx→∞ |
| = |
| =1 |
| | x+3 | | 1+3/x | |
5 gru 16:23
Hajtowy: Czemu mi pomysł zabrałeś?

5 gru 16:28
Hajtowy:

| | 3x3+2 | | 3x3−1+3 | |
u) limx→∞ ( |
| )x3+2x = limx→∞ ( |
| )x3+2x = |
| | 3x3−1 | | 3x3−1 | |
| | 3 | | 3x3 .... | | −3(....) | |
=limx→∞ [ (1 − |
| ) |
| ] |
| =e.... |
| | 3x3−1 | | −3.... | | 3x3−1 | |
Tam gdzie są .... mam dylemat co tam wpisać

5 gru 16:43
jakubs: | | 3x3−1 | | −3 | |
w potędze |
| * |
| * x3+2x |
| | −3 | | 3x3−1 | |
5 gru 16:47
Hajtowy: Oblicz granicę jednostronną funkcji

Co z tym zrobić?

5 gru 17:39
jakubs: Jednostronne czyli:
5 gru 17:44
Hajtowy: A teraz pytanie... dlaczego przy jednym zerze jest + a przy drugim − ?
Jak to rozpoznać?
5 gru 17:45
jakubs: | | 10000001 | |
1+ wyobraź sobie jako np. |
| , coś delikatnie większego od 1. |
| | 10000000 | |
| | 2 | | 10000000 | |
np. |
| = 2 * |
| |
| | | | 10000001 | |
| | 100000001 | |
1− analogicznie np. − |
| |
| | 100000000 | |
Lepiej aby Ci ktoś inny to wytłumaczył, abym Ci w głowie nie namieszał, ale ja to sobie tak
interpretuję i mi jest z tym dobrze

Oczywiście danych wartości nie podstawiamy, tylko chciałem Ci to jakoś pokazać.
5 gru 17:51
jakubs: Kurde źle, jeszcze tam trzeba odjąć 1 czyli np.(dla zobrazowania)
| | 10000001 | | 10000000 | | 1 | |
[1+−1] −> |
| − |
| = |
| |
| | 10000000 | | 10000000 | | 10000000 | |
5 gru 17:52
Hajtowy: Witam ponownie

Obliczyć granice jednostronną funkcji

| | x2−4 | |
c) f(x)= |
| ; x0 = 2 |
| | x2−4x+4 | |
| | x2−4 | | 0 | |
limx→2+ = |
| = [ |
| ] |
| | x2−4x+4 | | 0 | |
| | x2−4 | | 0 | |
limx→2− = |
| = [ |
| ] |
| | x2−4x+4 | | 12 | |
I teraz gdzie plus gdzie minus

7 gru 10:47
52:
Ok...
Robię, ale niech sprawdzi to "fachowiec"
| | (x−2)(x+2) | | x+2 | |
f(x)= |
| = |
| |
| | (x−2)2 | | x−2 | |
| | x+2 | | 4 | |
limx→2+ |
| =[ |
| ]= ?  |
| | x−2 | | 0+ | |
| | x+2 | | 4 | |
limx→2− |
| =[ |
| ]=... |
| | x−2 | | 0− | |
7 gru 11:45
Hajtowy: Na górze +
∞, na dole −
∞ ?

7 gru 11:55
Hajtowy:
| | |2x−1| | | 1 | |
d) f(x) = |
| ; x0= |
| |
| | 2x−1 | | 2 | |
| | |2x−1| | |
limx→1/2 + |
| = ... |
| | 2x−1 | |
| | |2x−1| | |
limx→1/2 + |
| = ... |
| | 2x−1 | |
a co z tym zrobić?

7 gru 12:00
52: 11:55 tak...
| | 1 | |
z lewej strony |
| moduł<0 zatem zmieniasz znaki ... |
| | 2 | |
| | 1 | |
z prawej strony |
| moduł>0 zatem zostawiasz znaki ... |
| | 2 | |
7 gru 12:03
Hajtowy:
prawa strona wyszła mi 1
lewa strona zaś −1

7 gru 12:06
52: ta
7 gru 12:08
jakubs: 
7 gru 12:08
Hajtowy:
| | sinx | | sinx | | 1 | | 1 | |
limx→0+ |
| = |
| = |
| = [ |
| ] = +∞ |
| | x2 | | x*x | | x | | 0 | |
| | sinx | | sinx | | 1 | | 1 | |
limx→0− |
| = |
| = |
| = [ |
| ] = −∞ |
| | x2 | | x*x | | x | | 0 | |
Tak?

7 gru 12:09
52: mhh..
tylko warto by dać
| | 1 | |
[ |
| ]=+∞ i analogicznie do minus.. |
| | 0+ | |
7 gru 12:11
Hajtowy:
A taki przykład...?


1/x to potęga e
7 gru 12:14
52: Nie wiem...
7 gru 12:20
Hajtowy:
No to mam jeszcze 3 przykłady...
| | ⎧ | (x2−3) / (x−2) dla x > 2 | |
| f(x) = | ⎨ | | ; x0 = 2
|
| | ⎩ | (x2−4) / (x−2) dla x < 2 | |
lim
x→2 3
(x−2) / (x2−4) (3 do potęgi x−2 przez x
2−4)
| | sin16x | |
limx→0 4√ |
| (pierwiastek 4 stopnia z całości) |
| | x | |
7 gru 12:33
Hajtowy: Trzeci wydaje się być najłatwiejszy, tylko przeszkadza mi ta 16 w liczniku


Nie wiem jak się tego pozbyć
7 gru 12:34
52: zacznijmy od pierwszego
lim
x→2−x+2=4
Nie wiem czy dobrze to robię..
lim
x→2 3
(x−2)/(x2−4)=lim
x→23
1/(x+2)=3
1/4
Niech ktoś to sprawdzi na wszelki wypadek..
Nie wiem jak ostatnie zrobić.. chociaż ja bym kombinował aby licznik i mianownik pomnożyć przez
4√16x
7 gru 12:41
Hajtowy: 2 przykład
4√3 ma wyjść i wyszło

7 gru 12:54
52: No to super a co jest z pierwszym źle ?
7 gru 12:55
Hajtowy: W pierwszym ma wyjść 4 i +
∞ czyli jest git

A jak trzecie zrobić?

7 gru 12:57
52: Czekaj spróbuję pierw na kartce ...
7 gru 12:59
52: Ok już mam
| | sin16x | | sin16x * 16x | |
limx→0 4√ |
| =limx→0 4√ |
| = |
| | x | | x * 16x | |
| | 16x | |
limx→0 4√ |
| = 4√16=2  |
| | x | |
7 gru 13:02
7 gru 13:04
52: Spoko, akurat mam z tego kolokwium w środę więc ... korzyść dla nas obu

7 gru 13:05
daras: @
Hajtowy na wykłądzie być może była tylko 1h może będzie wiecej w przyszłym tygodniu albo
na ćwiczeniach

ale w bibliotece można spędzić ze 100 godzin czytając podreczniki i
studiując przykładowe rozwiązania w zbiorach zadań, na tym polegały kiedyś studia, mam
nadzieję, że metoda się nie zestarzała bo przynosiła dobre rezultaty. Polecam dzieła rosyjskie
np. Liaszkę , a z polskich Krysickiego Włodarskiego czy śp. Plucińskiego z Gdowskim.
7 gru 13:06
52: daras niestety ma rację wykład trwa 1,5h tyle ile zdąży przepisać wykładowca ze skryptu
(czasem może wytłumaczy) tyle masz w zeszycie wszystkiego musisz się samemu uczyć czytając
właśnie książki... A szkoda że tak mało czasu jest przeznaczone na wytłumaczenie danego
zagadnienia na uczelni ...
7 gru 13:09
52: Chociaż jak dla mnie to dobrze że istnieje to forum to i tak przy czytaniu książek mi dużo
czasu nie zabiera... ale to tylko matematyka a gdzie inne przedmioty

7 gru 13:11
Hajtowy: Na wykładzie były macierze już (ominęliśmy wgl granice ciągów i funkcji...) profesor stwierdził
iż to było w szkole średniej i my to umiemy... a w czwartek mam kolosa na ćwiczeniach z granic
funkcji dlatego tak szybkiej pomocy potrzebowałem... Wiem, że mogę spędzić w bibliotece
mnóstwo godzin, ale jak ma się zajęcia 8−18 ; 8−16 ; 8−15:30 to się nie chce już później nic
robić, uwierz mi

Niestety program ćwiczeń jest inny a wykładów inny, przez to te problemy

7 gru 13:13
Mariusz: Co do dzieł rosyjskich to zgoda dobre są ale czy nie przestarzałe
Teraz jest moda na angielszczyznę
Te rosyjskie dzieła które widziałem pochodziły jeszcze z czasów Союза
12 gru 05:57
daras: i to był właśnie najlepiej poznany okres, od tamtej pory nie interesujemy się co za wschodnią
granicą piszą(czyt. knują) a to źle, bo trzeba wiedziec co sąsiad zza miedzy knuje , dzis
sąsiad a jutro wróg...moda na amerykanizmy nas jeszcze zgubi
@Hajtowy czy Ty sam studiujesz?
12 gru 10:42
daras: @13:13 wierzę, że już nic się nie chce robić tylko

ja tez z tego co pamiętam grałem w karty ( na szczęście nie było w pokoju ogłupiającej
TV

ani

) i

nie lubiłem siedzieć w czytelni(za cicho, teraz też nie
lubię bo za głośno−ciągle dzwonią komórki) nie chodziłem na wszystkie nudne wykłady, na
których niektórzy docenci przepisywali na tablicy te same książki, które mogłem wypożyczyć z
biblioteki i to nawet z błędami choć miały errary z tyłu, na spalonej pozycji były wszystkie
wykłady zaczynające się o 8:15 wolałem się

za to wieczorami lubiłem

i
porozwiązywać r−nia różniczkowe, bo nie byłem tak zmęczony

12 gru 10:52
Hajtowy: daras jest nas ponad 300 na I roku

12 gru 11:35
daras: a ile jest grup

12 gru 18:19
 Będzie miał ktoś jutro chęci i czas by poświęcić go na przerobienie ze mną kilkunastu zadań z
granicy funkcji do kolokwium?
Będzie miał ktoś jutro chęci i czas by poświęcić go na przerobienie ze mną kilkunastu zadań z
granicy funkcji do kolokwium? 




 Obliczyć granicę w punkcie:
Obliczyć granicę w punkcie:









 ( tylko popraw chochlika)
( tylko popraw chochlika)






 Czy coś innego ?
Czy coś innego ?  Co by nie było dalej i tak jest KŁOPOT
Co by nie było dalej i tak jest KŁOPOT 


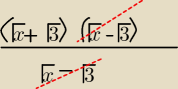
 nie zauważyłem tego
nie zauważyłem tego 





 wynik mam dobry xd
wynik mam dobry xd

 Bo nie wiem co dalej
Bo nie wiem co dalej 

 zaraz pokombinuje
zaraz pokombinuje 



 a już miałam to samo pisać ( Mila
a już miałam to samo pisać ( Mila 



 Bo tutaj chyba trzeba do 3 potęgi zastosować
Bo tutaj chyba trzeba do 3 potęgi zastosować 



 Magiczne ale jakże fajne i prawdziwe
Magiczne ale jakże fajne i prawdziwe 

 ten pierwiastek mi
przeszkadza xd
ten pierwiastek mi
przeszkadza xd 








 Niestety jutrzejszy wf na 7:00 zmusza mnie do GŁĘBOKIEGO
Niestety jutrzejszy wf na 7:00 zmusza mnie do GŁĘBOKIEGO 
 aby się wyspać
aby się wyspać  Dziękuję wszystkim za pomoc dzisiejszą
Dziękuję wszystkim za pomoc dzisiejszą 
 Jutro się odezwę!
Jutro się odezwę! 

 Nowy dzień, nowe wyzwania
Nowy dzień, nowe wyzwania 
 policz jeszcze raz 1−1
policz jeszcze raz 1−1 

 Nawet 0 wychodzi z tego xd
Nawet 0 wychodzi z tego xd 

 <zalmka> takie głupie błędy...
No ale lecim dalej!
<zalmka> takie głupie błędy...
No ale lecim dalej! 







 (x+1)(√x+5+(x+3)) ≠ x2+2x+1−(x+5+x+3)
(x+1)(√x+5+(x+3)) ≠ x2+2x+1−(x+5+x+3)
 , skoro (x+1) się skróci,
−x2−5x−4≠ −((x+4)(x−1))
tylko
−(x2+5+4)=−(x+1)(x+4)
, skoro (x+1) się skróci,
−x2−5x−4≠ −((x+4)(x−1))
tylko
−(x2+5+4)=−(x+1)(x+4)




 tak się zastanawiam co to wgl jest xd
tak się zastanawiam co to wgl jest xd  Wiem, że gdy
Wiem, że gdy





 xD
xD 





 Ale wyszło pięknie
Ale wyszło pięknie 





 bo dla mnie to
ciężkie na poczatku
bo dla mnie to
ciężkie na poczatku 

 Ty jednak jakubs myślisz dobrze
Ty jednak jakubs myślisz dobrze 

 No to lecim dalej!
No to lecim dalej! 




 Robie dalej inne, jak bd miał problem to napiszę
Robie dalej inne, jak bd miał problem to napiszę 
 Zaplątałem się w przykładzie N
Zaplątałem się w przykładzie N 


 13 przykładów z tego typu zadań i to mnie zatrzymało...
no kurde no nie wiem!
13 przykładów z tego typu zadań i to mnie zatrzymało...
no kurde no nie wiem! 
 ?
?














 przykład Q
przykład Q  q) limx→∞ 3√x3+2x2−3√x3−2
Wiem, że mogę to sprzężeniem zrobić, ale też jest wzór na a3−b3? Dobrze kojarzę?
q) limx→∞ 3√x3+2x2−3√x3−2
Wiem, że mogę to sprzężeniem zrobić, ale też jest wzór na a3−b3? Dobrze kojarzę?
 dzięki
dzięki 












 Oczywiście danych wartości nie podstawiamy, tylko chciałem Ci to jakoś pokazać.
Oczywiście danych wartości nie podstawiamy, tylko chciałem Ci to jakoś pokazać.
 Obliczyć granice jednostronną funkcji
Obliczyć granice jednostronną funkcji 

 Ok...
Robię, ale niech sprawdzi to "fachowiec"
Ok...
Robię, ale niech sprawdzi to "fachowiec"









 Nie wiem jak się tego pozbyć
Nie wiem jak się tego pozbyć

 A jak trzecie zrobić?
A jak trzecie zrobić? 


 Dzięki
Dzięki 



 ale w bibliotece można spędzić ze 100 godzin czytając podreczniki i
studiując przykładowe rozwiązania w zbiorach zadań, na tym polegały kiedyś studia, mam
nadzieję, że metoda się nie zestarzała bo przynosiła dobre rezultaty. Polecam dzieła rosyjskie
np. Liaszkę , a z polskich Krysickiego Włodarskiego czy śp. Plucińskiego z Gdowskim.
ale w bibliotece można spędzić ze 100 godzin czytając podreczniki i
studiując przykładowe rozwiązania w zbiorach zadań, na tym polegały kiedyś studia, mam
nadzieję, że metoda się nie zestarzała bo przynosiła dobre rezultaty. Polecam dzieła rosyjskie
np. Liaszkę , a z polskich Krysickiego Włodarskiego czy śp. Plucińskiego z Gdowskim.

 Niestety program ćwiczeń jest inny a wykładów inny, przez to te problemy
Niestety program ćwiczeń jest inny a wykładów inny, przez to te problemy
 ja tez z tego co pamiętam grałem w karty ( na szczęście nie było w pokoju ogłupiającej
TV
ja tez z tego co pamiętam grałem w karty ( na szczęście nie było w pokoju ogłupiającej
TV ani
ani  ) i
) i  nie lubiłem siedzieć w czytelni(za cicho, teraz też nie
lubię bo za głośno−ciągle dzwonią komórki) nie chodziłem na wszystkie nudne wykłady, na
których niektórzy docenci przepisywali na tablicy te same książki, które mogłem wypożyczyć z
biblioteki i to nawet z błędami choć miały errary z tyłu, na spalonej pozycji były wszystkie
wykłady zaczynające się o 8:15 wolałem się
nie lubiłem siedzieć w czytelni(za cicho, teraz też nie
lubię bo za głośno−ciągle dzwonią komórki) nie chodziłem na wszystkie nudne wykłady, na
których niektórzy docenci przepisywali na tablicy te same książki, które mogłem wypożyczyć z
biblioteki i to nawet z błędami choć miały errary z tyłu, na spalonej pozycji były wszystkie
wykłady zaczynające się o 8:15 wolałem się  za to wieczorami lubiłem
za to wieczorami lubiłem  i
porozwiązywać r−nia różniczkowe, bo nie byłem tak zmęczony
i
porozwiązywać r−nia różniczkowe, bo nie byłem tak zmęczony

