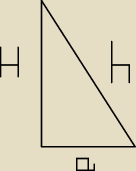Witam. Mam problem z rozwiązaniem tego zadania. Sciany boczne ostrosłupa prawidłowego
czworokątnego są nachylone do podstawy pod kątek 60 stopni. Pole powierzchni ostrosłupa wynosi
48. Oblicz objętość tego ostrosłupa.
H − wysokość bryły
h − wysokość ściany bocznej
a − połowa dł. podstawy
teraz z trójkątów o stopniach 90, 60, 30 wynika, że
H − 1/2a√3
h − 2a − a
1/2a − a
Podstawiam to do wzoru na Pc 48 = a2 + 4 * (a*h/2) zamiast h podstawiam nasze a, bo to to samo
według naszych wcześniejszych obliczeń i chcę obliczyć a. Natomiast a wychodzi mi tak a=√9,6 i
nie wiem co jest źle i jak ruszyć dalej to zadanie...
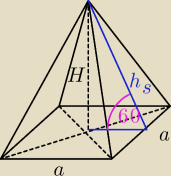Pc = a2 + 2a*hs = 48
| a2 | 1 | ||
= cos60o = | |||
| hs | 2 |
| √3 | ||
H = hs*sin60o = a* | = 2√3 | |
| 2 |
| a2H | 32 | |||
V = | = | √3 | ||
| 3 | 3 |
