Funkcja wymierna z wartością bezwzględną. Kolorowy: Jak narysować taką funkcję wymierną z wartością bezwzględną:

	2
y=I		−2I
	IxI + 3

pigor: ..., przekształć wzór w 2−óch przypadkach : 1) dla x<0; 2) dla x≥0 i rysuj (części wykresów funkcji homograficznej) w tych przedziałach; a inaczej ja najpierw sobie przekształcę i zobaczę do czego dojdę np. tak:

	2		2−2|x|−6		|x|+2
y=|f(x)| , gdzie f(x)=		− 2=		= −2*		=
	|x|+3		|x|+3		|x|+3

	|x|+3−1		1
= −2*		= −2(1−		) , czyli masz do narysowania
	|x|+3		|x|+3

	2
wykres funkcji parzystej f(x)= −2+		(rysujesz jej wykres tylko dla
	|x|+3

x≥0 najlepiej przerywaną linią i tę część odbijasz symetrycznie względem osi OY) ; jak już to zrobisz, to wykres danej funkcji y=|f(x)| zapewne już prosta sprawa co ...

Mila:

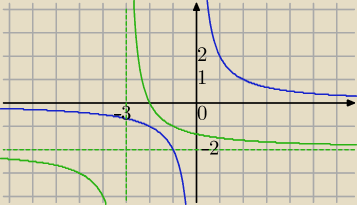
	2		2
1) g(x)=		→T[−3,−2]→h(x)=		−2
	x		x+3

Dalej na następnym rysunku

Mila:

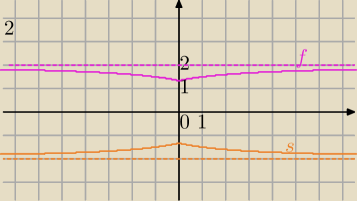
	2		2
1) g(x)=		→T[−3,−2]→h(x)=		−2
	x		x+3

cd

	2		2
2)h(x)=		−2→SOY tylko wykresu z prawej strony OY⇒s(x)=		−2→
	x+3		|x|+3

	2
SOX⇒f(x)=|		−2|
	|x|+3

Kacper: Ja tylko zwrócę uwagę, na to, że przekształceń 2 i 3 u Mili nie można przestawić Mila

Mila: