geometria analityczna koło cytrynka: Dla jakich wartości parametru m m € R proste k: x+y−m−1=0 i p: 2x+y−2m=0 przecinają się w punkcie który należy do koła o środku S (0,1) i promieniu r=p {10}

cytrynka: Wiem, że równanie okręgu to x²+(y−1)²=10

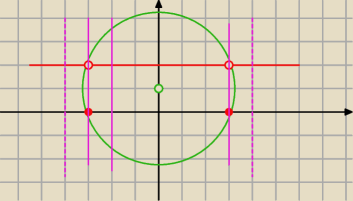
+-: ... to poszukajmy współrzędnych punktu przecięcia się tych prostych Zatem: x+y−m−1=2x+y−2m ⇒ x=m−1 y+m−1−m−1=0 ⇒ y=2 Poste te przecinają się więc na prostej y=2 Poszukajmy odcinka leżącego na tej prostej jednocześnie należącego do koła x²+(y−1)²=10 x²+(2−1)²=10 x=−3 x=3 a więc −3≤m−1≤3 ⇒ −2≤m≤4